
���� ��1������������߷�����c=1������Բ��������e=$\frac{c}{a}$=$\frac{{\sqrt{2}}}{2}$���������a��b��ֵ�������Բ���̣�
��2����i����ֱ�߷��̴�����Բ���̣�����Τ�ﶨ�������ֱ�ߵ�б�ʹ�ʽ���ɵ�m=-2k�������õ�ֱ�ߺ�����㣨2��0����
��ii�������ҳ���ʽ���حMNح����|MG|=|NG|��G���߶�MN���д����ϣ�ֱ��GD�ķ��̣����m2=$\frac{{k}^{2}{t}^{2}}{��2{k}^{2}+1��^{2}}$���������û�������ʽ�����ʣ��������ʵ��m��ȡֵ��Χ��
��� �⣺��1���������֪����Բ��������e=$\frac{c}{a}$=$\frac{{\sqrt{2}}}{2}$����a=$\sqrt{2}$c��
������y2=-4x�߷���x=1����c=1��
��a=$\sqrt{2}$��b=$\sqrt{{a}^{2}-{c}^{2}}$=1��
����Բ�ı����̣�$\frac{{x}^{2}}{2}+{y}^{2}=1$��
��2����M��x1��y1����N��x2��y2����
��$\left\{\begin{array}{l}{y=kx+t}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$���������1+2k2��x2+4ktx+2t2-2=0��
���=16k2t2-8��1+2k2����t2-1����0��
��x1+x2=-$\frac{4kt}{1+2{k}^{2}}$��x1x2=$\frac{2{t}^{2}-2}{1+2{k}^{2}}$��
��i��֤������k1+k2=$\frac{{y}_{1}}{{x}_{1}-1}$+$\frac{{y}_{2}}{{x}_{2}-1}$=$\frac{k{x}_{1}+t}{{x}_{1}-1}$+$\frac{k{x}_{2}+t}{{x}_{2}-1}$=0��
��2kx1x2-2t+��t-k����x1+x2��=0��
����Τ�ﶨ�����ɵ�2k•$\frac{2{t}^{2}-2}{1+2{k}^{2}}$-2t+��t-k����-$\frac{4kt}{1+2{k}^{2}}$��=0��
����ɵ�t=-2k��
��ֱ�ߵķ���Ϊy=kx-2k����y=k��x-2����
��ֱ��l������㣨2��0����
��ii��������ڵ�G��m��0�������������⣬حMNح=$\sqrt{1+{k}^{2}}$•$\sqrt{��{x}_{1}+{x}_{2}��^{2}-4{x}_{1}{x}_{2}}$��
��حMNح=$\frac{2\sqrt{2}\sqrt{{k}^{2}+1}•\sqrt{2{k}^{2}+1-{t}^{2}}}{2{k}^{2}+1}$=2��
����������t2=$\frac{2{k}^{2}+1}{2��{k}^{2}+1��}$��
��ʱ�б�ʽ��=8��2k2+1-t2��=8[2k2+1-$\frac{2{k}^{2}+1}{2��{k}^{2}+1��}$]��0�������
��k��R��
��MN�е�D��x0��y0������x0=$\frac{{x}_{1}+{x}_{2}}{2}$=-$\frac{2kt}{2{k}^{2}+1}$��y0=$\frac{t}{2{k}^{2}+1}$��
��|MG|=|NG|����G���߶�MN���д����ϣ�
��k��0��ֱ��GD�ķ���Ϊy-$\frac{t}{2{k}^{2}+1}$=-$\frac{1}{k}$��x+$\frac{2kt}{2{k}^{2}+1}$������y=0���ɵ�m=-$\frac{kt}{2{k}^{2}+1}$��
��m2=$\frac{{k}^{2}{t}^{2}}{��2{k}^{2}+1��^{2}}$��
��m2=$\frac{{k}^{2}}{2{��k}^{2}+1����2{k}^{2}+1��}$=$\frac{1}{2��2{k}^{2}+\frac{1}{{k}^{2}}+3��}$��
��m2��$\frac{1}{2��2\sqrt{2{k}^{2}•\frac{1}{{k}^{2}}+3}��}$=$\frac{1}{2��2\sqrt{2}+3��}$=$\frac{1}{��\sqrt{2}��^{2}��\sqrt{2}+1��^{2}}$��
��حmح��$\frac{2-\sqrt{2}}{2}$����m��0��
��m��ȡֵ��ΧΪ[-$\frac{2-\sqrt{2}}{2}$���ȣ�0��$\frac{2-\sqrt{2}}{2}$]��
��k=0ʱ��m=0��
���ϣ�m��ȡֵ��ΧΪ[-$\frac{2-\sqrt{2}}{2}$��$\frac{2-\sqrt{2}}{2}$]��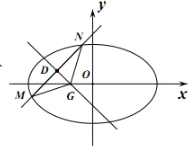
���� ���⿼����Բ�ķ��̵�������ֱ�ߺ���������ע����������ֱ�߷��̺���Բ���̣�����Τ�ﶨ����ֱ�ߵ�б�ʹ�ʽ��ע�����õȱ����е���������ʺ�Τ�ﶨ�����ҳ���ʽ���е����깫ʽ����������ʽ���ۺ�Ӧ�ã����黯�����������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 2 | C�� | 20 | D�� | 4034 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | P��Q | B�� | ���VP����Q | C�� | ���VP���ģ��VQ�� | D�� | P�ģ��VQ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
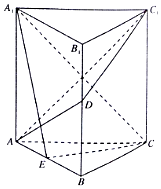 ��ͼ����������ABC-A1B1C1�������ⳤ��Ϊ2��DΪ��BB1��һ�㣬E��AB���е㣮
��ͼ����������ABC-A1B1C1�������ⳤ��Ϊ2��DΪ��BB1��һ�㣬E��AB���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
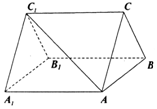 ��ͼ��ʾ���������У�����ABB1A1Ϊ�߳�����2�����Σ��ҡ�AA1B1=60�㣬��ABCΪ�ȱ������Σ���ABC����ABB1A1��
��ͼ��ʾ���������У�����ABB1A1Ϊ�߳�����2�����Σ��ҡ�AA1B1=60�㣬��ABCΪ�ȱ������Σ���ABC����ABB1A1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{4}$ | B�� | $\frac{7}{16}$ | C�� | $\frac{1}{2}$ | D�� | $\frac{9}{16}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com