
【题目】动圆M与圆(x﹣1)2+y2=1相外切且与y轴相切,则动圆M的圆心的轨迹记C,
(1)求轨迹C的方程;
(2)定点A(3,0)到轨迹C上任意一点的距离|MA|的最小值;
(3)经过定点B(﹣2,1)的直线m,试分析直线m与轨迹C的公共点个数,并指明相应的直线m的斜率k是否存在,若存在求k的取值或取值范围情况[要有解题过程,没解题方程只有结论的只得结论分].
【答案】
(1)解:设动圆圆心M的坐标为(x,y),则 ![]() ,
,
∴(x﹣1)2+y2=x2+2|x|+1,
当x<0时,y=0;当x≥0时,y2=4x
(2)解:如图,由图可知,M到轨迹C上的点与A的距离最小,则M在抛物线y2=4x上,
设M(x,y),则|MA|= ![]() =
= ![]() =
= ![]() .
.
∴当x=1,即M(1,±2)时,|MA|的最小值为2 ![]()
(3)解:设过B与抛物线y2=4x相切的直线方程为y﹣1=k(x+2),即y=kx+2k+1,
联立 ![]() ,得k2x2+(4k2+2k﹣4)x+4k2+4k+1=0.
,得k2x2+(4k2+2k﹣4)x+4k2+4k+1=0.
由△=(4k2+2k﹣4)2﹣4k2(4k2+4k+1)=0,解得:k=﹣1或k= ![]() .
.
∴当直线m的斜率k不存在时或斜率存在为0时或直线m的斜率k∈( ![]() ,+∞)∪(﹣∞,﹣1)时,m与C有1个交点;
,+∞)∪(﹣∞,﹣1)时,m与C有1个交点;
当直线m的斜率为k=﹣1或k= ![]() 或k∈[﹣
或k∈[﹣ ![]() ,0)时,m与C有2个交点;
,0)时,m与C有2个交点;
当直线m的斜率k∈(0, ![]() )∪(﹣1,﹣
)∪(﹣1,﹣ ![]() )时,m与C有3个交点.
)时,m与C有3个交点.
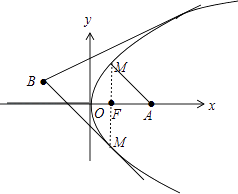
【解析】(1)设出动圆圆心M的坐标,利用动圆M与y轴相切且与圆(x﹣1)2+y2=1外切建立方程,化简得答案;(2)设M的坐标,利用两点间的距离公式结合配方法求得定点A(3,0)到轨迹C上任意一点的距离|MA|的最小值;(3)写出过B斜率存在的直线方程,联立直线方程与抛物线方程,由判别式等于0求得k值,再结合图形求得直线m与轨迹C的公共点个数,并分析对应的斜率情况.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 是定义在(﹣1,1)上的奇函数,且f(
是定义在(﹣1,1)上的奇函数,且f( ![]() )=
)= ![]() ,则不等式f(t﹣1)+f(t)<0的解集为( )
,则不等式f(t﹣1)+f(t)<0的解集为( )
A.(0,1)
B.(0, ![]() ]
]
C.(0, ![]() )
)
D.( ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)两个共轭复数的差是纯虚数;(2)两个共轭复数的和不一定是实数;(3)若复数a+bi(a,b∈R)是某一元二次方程的根,则a﹣bi是也一定是这个方程的根;(4)若z为虚数,则z的平方根为虚数,
其中正确的个数为( )
A.3
B.2
C.1
D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100 个网箱,测量各箱水产品的产量(单位:kg).其频率分布直方图如下:
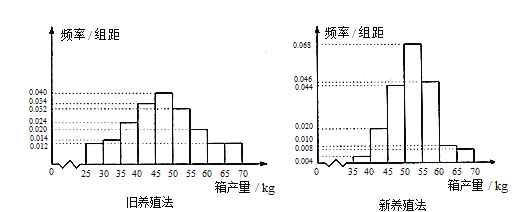
(1)设两种养殖方法的箱产量相互独立,记A表示事件:“旧养殖法的箱产量低于50kg,新养殖法的箱产量不低于50kg”,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
箱产量<50kg | 箱产量≥50kg | |
旧养殖法 | ||
新养殖法 |
(3)根据箱产量的频率分布直方图,求新养殖法箱产量的中位数的估计值(精确到0.01).
附: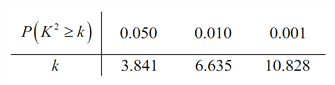 ,
, 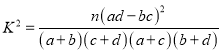
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1= ![]() 且an+1=an﹣an2(n∈N*)
且an+1=an﹣an2(n∈N*)
(1)证明:1< ![]() ≤2(n∈N*);
≤2(n∈N*);
(2)设数列{an2}的前n项和为Sn , 证明 ![]() (n∈N*).
(n∈N*).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)的解析式满足 ![]() .
.
(1)求函数f(x)的解析式;
(2)当a=1时,试判断函数f(x)在区间(0,+∞)上的单调性,并加以证明;
(3)当a=1时,记函数 ![]() ,求函数g(x)在区间
,求函数g(x)在区间 ![]() 上的值域.
上的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com