
分析 (1)由题意可得B=120°,A+C=60°.再利用积化和差公式化简sinAsinC 为$\frac{1}{2}$cos(A-C)-$\frac{1}{4}$.再根据再根据-60°<A-C<60°,利用余弦函数的定义域和值域求得sinAsinC的取值范围.
(2)由条件利用余弦定理、基本不等式求得ac的最大值,从而求得△ABC面积的最大值的最大值.
解答 解:(1)△ABC中,由cosB=-$\frac{1}{2}$,可得B=120°,A+C=60°.
∴sinAsinC=$\frac{1}{2}$[cos(A-C)-cos(A+C)]=$\frac{1}{2}$[cos(A-C)-$\frac{1}{2}$]=$\frac{1}{2}$cos(A-C)-$\frac{1}{4}$.
再根据-60°<A-C<60°,可得cos(A-C)∈($\frac{1}{2}$,1),$\frac{1}{2}$cos(A-C)∈($\frac{1}{4}$,$\frac{1}{2}$),
∴$\frac{1}{2}$cos(A-C)-$\frac{1}{4}$∈(0,$\frac{1}{4}$),即sinAsinC的取值范围为(0,$\frac{1}{4}$).
(2)若b=2$\sqrt{3}$,由余弦定理可得b2=12=a2+c2-2ac•cosB≥2ac+ac=3ac,
即ac≤4,当且仅当a=c=2时,取等号,故ac的最大值为4,
故△ABC面积为$\frac{1}{2}$ac•sin120°≤$\sqrt{3}$.
点评 本题主要考查积化和差公式、余弦定理、余弦函数的定义域和值域,基本不等式的应用,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{5}$,7] | B. | [$\frac{1}{7}$,5] | C. | (-∞,$\frac{1}{5}$]∪[7,+∞] | D. | (-∞,$\frac{1}{7}$]∪[5,+∞] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
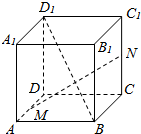 如图所示,在正方体ABCD一A1B1C1D1中,取$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$作为基底.
如图所示,在正方体ABCD一A1B1C1D1中,取$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$作为基底.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | aπ | B. | |a|π | C. | $\frac{π}{a}$ | D. | $\frac{π}{|a|}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com