(1)解:令x=y=0,∵f(0)>0,
∴f(0)=f(0×0)=[f(0)]
0=1.
(2)证明:∵f(1)=
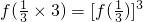
,
∵
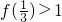
,∴f(1)>1.
∵对任意的x,y∈R,f(xy)=[f(x)]
y;
令x=1,则f(y)=[f(1)]
y,
再令y=x,则f(x)=[f(1)]
x.
(3)解:∵f(1)>1,∴f(x)=[f(1)]
x是R上的增函数,
∵f(3
x)-f(9
x-3
x+1-2k)>0对任意的x∈[0,1]恒成立,
∴3
x>9
x-3
x+1-2k对x∈[0,1]恒成立.
即2k>9
x-4×3
x对x∈[0,1]恒成立.
令g(x)=9
x-4×3
x=(3
x)
2-4×3
x=(3
x-2)
2-4在[0,1]上单调递减,
∴g(x)
max=g(0)=-3.∴2k>-3.
∴
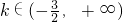
.
分析:(1)利用所给条件(1)(2)即可得出;
(2)令x=

,y=3,代入条件(2),再利用(3)即可得出.对任意的x,y∈R,f(xy)=[f(x)]
y;分别取x=1之后,再令y=x即可.
(3)利用(2)的结论可得:f(x)=[f(1)]
x是R上的增函数,即可得出3
x>9
x-3
x+1-2k对x∈[0,1]恒成立.通过分离参数可得2k>9
x-4×3
x对x∈[0,1]恒成立.利用二次函数的单调性即可得出.
点评:正确理解和应用新定义、函数的单调性、指数函数的单调性等是解题的关键.

 )>1;利用以上信息求解下列问题:
)>1;利用以上信息求解下列问题: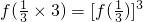 ,
,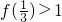 ,∴f(1)>1.
,∴f(1)>1.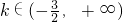 .
. ,y=3,代入条件(2),再利用(3)即可得出.对任意的x,y∈R,f(xy)=[f(x)]y;分别取x=1之后,再令y=x即可.
,y=3,代入条件(2),再利用(3)即可得出.对任意的x,y∈R,f(xy)=[f(x)]y;分别取x=1之后,再令y=x即可.

