
(本小题满分12分)
如图,ABCD为梯形,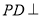 平面ABCD,AB//CD,
平面ABCD,AB//CD,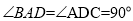
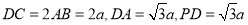 ,E为BC中点,连结AE,交BD于O.
,E为BC中点,连结AE,交BD于O.
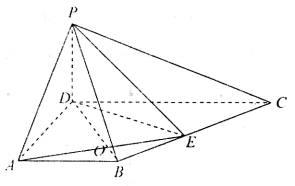
(I)平面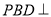 平面PAE
平面PAE
(II)求二面角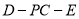 的大小(若非特殊角,求出其余弦即可)
的大小(若非特殊角,求出其余弦即可)
(1)见解析;(2)
【解析】
试题分析:(1)证明两个平面垂直,首先考虑直线与平面垂直,也可以简单记为“证面面垂直,找线面垂直”,是化归思想的体现,这种思想方法与空间中的平行关系的证明类似,掌握化归与转化思想方法是解决这类题的关键;(2)作二面角的平面角可以通过垂线法进行,在一个半平面内找一点作另一个平面的垂线,再过垂足作二面角的棱的垂线,两条垂线确定的平面和二面角的棱垂直,由此可得二面角的平面角.
试题解析:(Ⅰ)连结


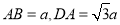 ,所以
,所以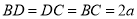
 为
为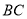 中点,所以,
中点,所以,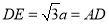
因为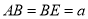 ,
,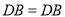
所以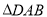 与
与 为全等三角形
为全等三角形
所以
所以 与
与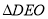 为全等三角形
为全等三角形
所以在 中,
中,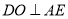 ,即
,即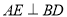 3分
3分
又因为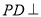 平面
平面 ,
, 平面
平面
所以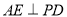 4分
4分
而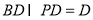
所以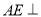 平面
平面 5分
5分
因为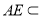 平面
平面
所以平面 平面
平面 6分
6分
(Ⅱ) 以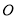 为原点,分别以
为原点,分别以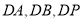 所在直线为
所在直线为 轴,建立空间直角坐标系如图
轴,建立空间直角坐标系如图

二面角 即二面角
即二面角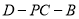
 平面
平面 ,平面
,平面 的法向量可设为
的法向量可设为
 7分
7分
设平面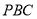 的法向量为
的法向量为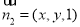
所以 ,而
,而

即: ,可求得
,可求得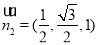 10分
10分

所以两平面 与平面
与平面 所成的角的余弦值
所成的角的余弦值
为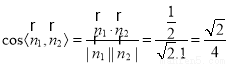 12分
12分
考点:空间几何的位置关系.


科目:高中数学 来源:2014-2015学年上海市青浦区高三上学期期终学习质量调研数学试卷(解析版) 题型:填空题
若甲乙两人从 门课程中各选修
门课程中各选修 门,则甲乙所选的课程中恰有
门,则甲乙所选的课程中恰有 门相同的选法有 种.
门相同的选法有 种.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省青岛市高三上学期期末考试理科数学试卷(解析版) 题型:选择题
若圆台两底面周长的比是1:4,过高的中点作平行于底面的平面,则圆台被分成两部分的体积比是
A.1:16 B.39:129 C.13:129 D.3:27
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省无锡市高三上学期期末考试文科数学试卷(解析版) 题型:填空题
将函数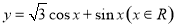 的图像向左平移个
的图像向左平移个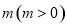 单位长度后,所得的图像关于
单位长度后,所得的图像关于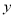 轴对称,则
轴对称,则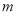 的最小值是
的最小值是
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河南省信阳市毕业班第二次调研检测文科数学试卷(解析版) 题型:选择题
已知函数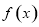 的定义域为
的定义域为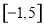 ,部分对应值如下表,
,部分对应值如下表,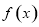 的导函数y=
的导函数y=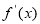 的图象如图所示.
的图象如图所示.
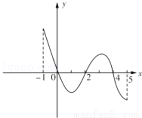
x | -1 | 0 | 2 | 4 | 5 |
y | 1 | 2 | 0 | 2 | 1 |
若函数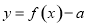 有
有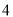 个零点,则实数
个零点,则实数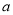 的取值范围为( )
的取值范围为( )
(A)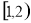 (B)
(B)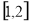 (C)
(C) 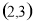 (D)
(D)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com