
【题目】已知f(x)=2ln(x+2)﹣(x+1)2 , g(x)=k(x+1).
(1)求f(x)的单调区间;
(2)当k=2时,求证:对于x>﹣1,f(x)<g(x)恒成立;
(3)若存在x0>﹣1,使得当x∈(﹣1,x0)时,恒有f(x)>g(x)成立,试求k的取值范围.
【答案】
(1)解: ![]() ,
,
当f′(x)>0 时,所以 x2+3x+1<0,解得﹣2<x,
当f′(x)<0时,解得 ![]() ,
,
所以 f(x) 单调增区间为 ![]() ,递减区间是(
,递减区间是( ![]() ,+∞);
,+∞);
(2)解:当k=2时,g(x)=2(x+1).
令H(x)=f(x)﹣g(x)=2ln(x+2)﹣(x+1)2﹣2(x+1).
H′(x)= ![]() ,
,
令H′(x)=0,即﹣2x2﹣8x﹣6=0,解得x=﹣1或x=﹣3(舍).
∴当x>﹣1时,H′(x)<0,H(x)在(﹣1,+∞)上单调递减.
∴Hmax(x)=H(﹣1)=0,
∴对于x>﹣1,H(x)<0,即f(x)<g(x).
(3)解:由(2)知,当k=2时,f (x)<g (x)恒成立,
即对于“x>﹣1,2 ln (x+2)﹣(x+1)2<2 (x+1),不存在满足条件的x0;
当k>2时,对于“x>﹣1,x+1>0,此时2 (x+1)<k (x+1).
∴2 ln (x+2)﹣(x+1)2<2 (x+1)<k (x+1),
即f (x)<g (x)恒成立,不存在满足条件的x0;
令h(x)=f(x)﹣g(x)=2ln(x+2)﹣(x+1)2﹣k(x+1),
h′(x)= ![]() ,
,
当k<2时,令t (x)=﹣2x2﹣(k+6)x﹣(2k+2),
可知t (x)与h′(x)符号相同,
当x∈(x0,+∞)时,t (x)<0,h′(x)<0,h (x)单调递减,
当x∈(﹣1,x0)时,h (x)>h (﹣1)=0,即f (x)﹣g (x)>0恒成立,
综上,k的取值范围为(﹣∞,2)
【解析】(1)求出定义域和导数f′(x),令f′(x)>0,解出增区间,令f′(x)<0,解出减区间;(2)令H(x)=f(x)﹣g(x),利用导数判断出H(x)的单调性和单调区间,得出H(x)的最大值,证明Hmax(x)<0即可.
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c.已知cos2A+ ![]() =2cosA.
=2cosA.
(1)求角A的大小;
(2)若a=1,求△ABC的周长l的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查某厂工人生产某种产品的能力,随机抽查了20位工人某天生产该产品的数量.产品数量的分组区间为[45,55),[55,65),[65,75),[75,85),[85,95)由此得到频率分布直方图如图.则产品数量位于[55,65)范围内的频率为;这20名工人中一天生产该产品数量在[55,75)的人数是 . 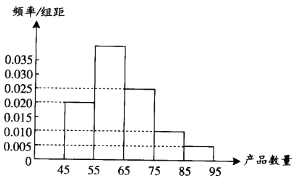
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cosxsin(x+![]() )﹣
)﹣![]() cos2x+
cos2x+![]() ,x∈R.
,x∈R.
(1)求f(x)的单调递增区间;
(2)在锐角△ABC中,角A,B,C的对边分别a,b,c,若f(A)=![]() ,a=
,a=![]() ,求△ABC面积的最大值.
,求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,半圆![]() 的直径为
的直径为![]() ,
, ![]() 为直径延长线上的一点,
为直径延长线上的一点, ![]() ,
, ![]() 为半圆上任意一点,以
为半圆上任意一点,以![]() 为一边作等边三角形
为一边作等边三角形![]() ,设
,设![]()
![]() .
.
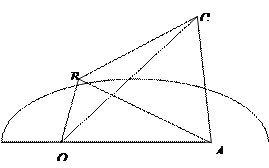
(1)当![]() 为何值时,四边形
为何值时,四边形![]() 面积最大,最大值为多少;
面积最大,最大值为多少;
(2)当![]() 为何值时,
为何值时, ![]() 长最大,最大值为多少.
长最大,最大值为多少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为正整数,数列
为正整数,数列![]() 满足
满足![]() ,
, ![]() ,设数列
,设数列![]() 满足
满足![]()
(1)求证:数列![]() 为等比数列;
为等比数列;
(2)若数列![]() 是等差数列,求实数
是等差数列,求实数![]() 的值;
的值;
(3)若数列![]() 是等差数列,前
是等差数列,前![]() 项和为
项和为![]() ,对任意的
,对任意的![]() ,均存在
,均存在![]() ,使得
,使得![]() 成立,求满足条件的所有整数
成立,求满足条件的所有整数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018海南高三阶段性测试(二模)】如图,在直三棱柱![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 上一动点.
上一动点.
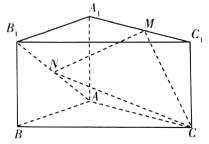
(I)是否存在一点![]() ,使得线段
,使得线段![]() 平面
平面![]() ?若存在,指出点
?若存在,指出点![]() 的位置,若不存在,请说明理由.
的位置,若不存在,请说明理由.
(II)若点![]() 为
为![]() 的中点且
的中点且![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校举办校园科技文化艺术节,在同一时间安排《生活趣味数学》和《校园舞蹈赏析》两场讲座.已知A、B两学习小组各有5位同学,每位同学在两场讲座任意选听一场.若A组1人选听《生活趣味数学》,其余4人选听《校园舞蹈赏析》;B组2人选听《生活趣味数学》,其余3人选听《校园舞蹈赏析》.
(1)若从此10人中任意选出3人,求选出的3人中恰有2人选听《校园舞蹈赏析》的概率;
(2)若从A、B两组中各任选2人,设X为选出的4人中选听《生活趣味数学》的人数,求X的分布列和数学期望E(X).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com