已知点A(-3,0),B(3,0),动点P满足|PA|=2|PB|,
(1)若点P的轨迹为曲线C,求此曲线的方程
(2)若点Q在直线l1:x+y+3=0上,直线l2经过点Q且与曲线C只有一个公共点M,求|QM|的最小值.
【答案】
分析:(1)设P点的坐标为(x,y),用坐标表示|PA|、|PB|,代入等式|PA|=2|PB|,整理即得点P的轨迹方程;
(2)求出圆心坐标,圆的半径,结合题意,利用圆的到直线的距离,半径,|QM|满足勾股定理,求出|QM|就是最小值.
解答:解:(1)设P点的坐标为(x,y),
∵两定点A(-3,0),B(3,0),动点P满足|PA|=2|PB|,
∴(x+3)
2+y
2=4[(x-3)
2+y
2],
即(x-5)
2+y
2=16.
所以此曲线的方程为(x-5)
2+y
2=16.
(2)∵(x-5)
2+y
2=16的圆心坐标为M′(5,0),半径为4,则圆心M′到直线l
1的距离为:
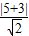
=4
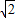
,
∵点Q在直线l
1:x+y+3=0上,过点Q的直线l
2与曲线C(x-5)
2+y
2=16只有一个公共点M,
∴|QM|的最小值为:
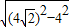
=4.
点评:考查两点间距离公式及圆的性质,着重考查直线与圆的位置关系,勾股定理的应用,考查计算能力,转化思想的应用,属于难题.

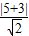 =4
=4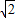 ,
,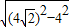 =4.
=4.

 如图,已知点A(
如图,已知点A(