
| A. | $2-\sqrt{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{π}{4}$ | D. | $\frac{2}{3}$ |
分析 根据题意,建立坐标系,设出A,B点的坐标,并设∠AOC=α,则由$\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$得x,y的值,从而求得x+y,结合正弦函数的性质可求满足条件的角α的范围,可求x+y≥$\sqrt{2}$的概率.
解答 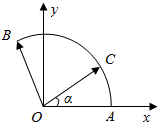 解:建立如图所示的坐标系,则A(1,0),B(cos120°,sin120°),
解:建立如图所示的坐标系,则A(1,0),B(cos120°,sin120°),
即B(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$)
设∠AOC=α,则$\overrightarrow{OC}$=(cosα,sinα)
∵$\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$=(x,0)+(-$\frac{1}{2}$y,$\frac{\sqrt{3}}{2}$y)=(cosα,sinα).
∴$\left\{\begin{array}{l}{x-\frac{1}{2}y=cosα}\\{\frac{\sqrt{3}}{2}y=sinα}\end{array}\right.$
∴x=$\frac{sinα}{\sqrt{3}}+cosα$,y=$\frac{2sinα}{\sqrt{3}}$
∴x+y=$\sqrt{3}$sinα+cosα=2sin(α+30°).
∵0°≤α≤120°.
∴30°≤α+30°≤150°.
当x+y≥$\sqrt{2}$时,可得sin(α+30°)≥$\frac{\sqrt{2}}{2}$
∴45°≤α+30°≤135°即15°≤α≤105°,
∴满足x+y≥$\sqrt{2}$的概率P$\frac{{{{120}°}-2×{{15}°}}}{{{{120}°}}}=\frac{3}{4}$
故选:B.
点评 本题是向量的坐标表示的应用,考查概率知识,结合图形,利用三角函数的性质,容易求出结果.


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
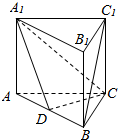 如图,在三棱柱A1B1C1中,四边形ABB1A1和ACC1A1都为矩形.
如图,在三棱柱A1B1C1中,四边形ABB1A1和ACC1A1都为矩形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a=-1 | B. | a=3 | C. | a=3或a=-1 | D. | a=3且a=-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
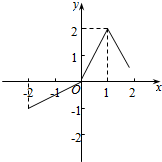
| A. | f(-2),0 | B. | 0,2 | C. | f(-2),2 | D. | f(2),2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com