考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定,二面角的平面角及求法
专题:空间位置关系与距离
分析:(1)取棱A1B1的中点E1,连结E1D,由已知得四边形DFB1E1为平行四边形,由此能证明B1F∥平面D1DE.
(2)取A1C1与B1D1的交点O1,在平面BB1D1D上作O1H⊥BD1,重足为H,连结HC1,∠O1HC1是所求二面角的平面角,由此能求出二面角C1-BD1-B1的大小.
(3)延长BA到M,使AM=AB,连结MD,则四边形MACD是平行四边形,当动点P与B重合时,P到平面DA1C1的距离最大,四面体DPA1C1体积最大.此时四面体DPA1C1为正四面体,由此能求出四面体DP1C1体积的最大值.
解答:
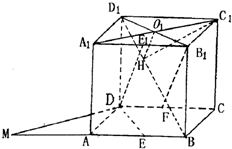
(1)证明:取棱A
1B
1的中点E
1,连结E
1D.
∵B
1E
1∥DF且相等,
∴四边形DFB
1E
1为平行四边形,∴B
1F∥DE
1.
又∵B
1F不包含于平面D
1DE,DE
1?平面D
1DE,
∴B
1F∥平面D
1DE.
(2)解:取A
1C
1与B
1D
1的交点O
1,
在平面BB
1D
1D上作O
1H⊥BD
1,重足为H,
连结HC
1.∵C
1O
1⊥B
1D
1,平面BB
1D
1D⊥平面A
1B
1C
1D
1,
∴C
1O
1⊥平面BB
1D
1D,∴C
1H⊥BD
1,
即∠O
1HC
1是所求二面角的平面角,
又C
1O
1=
a,
C1H==
a,
sin∠O
1HC
1=
=
,
∠O
1HC
1=60°,∴二面角C
1-BD
1-B
1的大小是60°.
(3)解:延长BA到M,使AM=AB连结MD,
∵AB∥DC且相等,
∴AM∥DC且相等,∴四边形MACD是平行四边形.
∴MD∥AC且相等,
又四边形A
1ACC
1是平行四边形,
∴AC∥A
1C
1且相等,
∴MD∥A
1C
1且相等,
∴MD与A
1C
1确定一个平面,即平面DA
1C
1,
∴M是直线BA与平面DA
1C
1的交点.
∴当动点P与B重合时,P到平面DA
1C
1的距离最大,
四面体DPA
1C
1体积最大.
此时四面体DPA
1C
1为正四面体,
棱长是
a,故四面体底面面积为
a2,高为
a,体积V=
a3.
点评:本题考查直线B1F∥平面D1DE的证明,考查二面角C1-BD1-B1的大小的求法,考查四面体DP1C1体积的最大值的求法,解题时要认真审题,注意空间思维能力的培养.

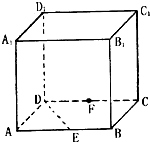 正方体ABCD-A1B1C1D1的棱长为a,E是棱AB的中点,F是棱CD的中点.
正方体ABCD-A1B1C1D1的棱长为a,E是棱AB的中点,F是棱CD的中点. (1)证明:取棱A1B1的中点E1,连结E1D.
(1)证明:取棱A1B1的中点E1,连结E1D.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案