已知函数f(x)=x2,x∈[-2,2]和函数g(x)=ax-1,x∈[-2,2],若对?x1∈[-2,2],总存在x0∈[-2,2],使f(x1)=g(x0)成立,则实数a的取值范围是________.
a≥2.5或a≤-2.5
分析:根据对于任意x
1∈[-2,2],总存在x
0∈[-2,2],使得g(x
0)=f(x
1)成立,得到函数f(x)在[-2,2],上值域是g(x)在[-2,2]上值域的子集,然后利用求函数值域的方法求函数f(x)、g(x)在[-2,2],上值域,并列出不等式,解此不等式组即可求得实数a的取值范围即可.
解答:①若a=0,g(x)=-1,对于任意 x
1∈[-2,2],f(x
1)∈[0,4],不存在x
0∈[-2,2],使g(x
0)=f(x
1)
②当a>0时,g(x)=ax-1在[-2,2]是增函数,g(x)∈[-2a-1,2a-1]
任给 x
1∈[-2,2],f(x
1)∈[0,4]
若存在x
0∈[-2,2],使得g(x
0)=f(x
1)成立
则
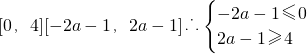
,∴

③a<0,g(x)=ax-1在[-2,2]是减函数,g(x)∈[2a-1,-2a-1]
∴
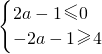
,∴
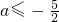
综上,实数a的取值范围是a≥2.5或a≤-2.5.
故答案为:a≥2.5或a≤-2.5
点评:本题主要考查了函数恒成立问题,以及函数的值域,同时考查了分类讨论的数学思想,属于中档题.

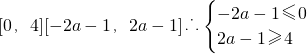 ,∴
,∴
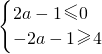 ,∴
,∴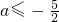


 阅读快车系列答案
阅读快车系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<