
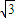 ,BD=
,BD=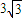 ,则AP= ,AC= .
,则AP= ,AC= .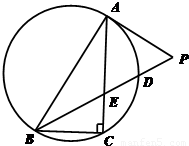
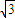 ,BD=3
,BD=3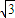 易得AP长;由∠ABC=60°结合弦切角定理易得△PAE为等边三角形,进而根据PE长求出AE长及ED,DB长,再根据相交弦定理可求出CE,进而得到答案.
易得AP长;由∠ABC=60°结合弦切角定理易得△PAE为等边三角形,进而根据PE长求出AE长及ED,DB长,再根据相交弦定理可求出CE,进而得到答案.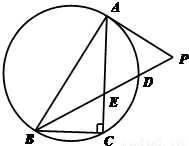 解:∵PD=
解:∵PD=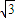 ,BD=3
,BD=3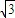 ,
,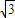 ,
,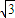 ,
,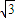
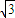
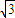
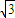 ,
,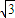 CE=6
CE=6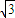
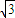 .
.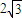 ;
;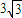 .
.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
 如图所示,在Rt△ABC中,∠CAB=90°,AB=2,AC=
如图所示,在Rt△ABC中,∠CAB=90°,AB=2,AC=
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源:设计必修三数学人教A版 人教A版 题型:013
在如图所示的Rt△ABC中,∠A=30°,过直角顶点C在∠ACB内任作一条射线交线段AB于M,则使AM>AC的概率是
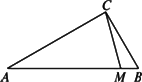
A.![]()
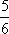

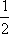
查看答案和解析>>
科目:高中数学 来源:单元双测 同步达标活页试卷 高二数学(下A) 人教版 题型:022
如图所示,Rt△ABC的直角顶点C在平面内,斜边AB∥α并且AB与α间的距离为![]() ,A、B在α内射影分别为D、E且DC=3,EC=4,则AB=________,∠DCE=________
,A、B在α内射影分别为D、E且DC=3,EC=4,则AB=________,∠DCE=________

查看答案和解析>>
科目:高中数学 来源:单元双测 同步达标活页试卷 高二数学(下A) 人教版 题型:044
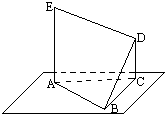
如图所示,Rt△ABC在平面α内,∠ABC=![]() ,AB=6,AD⊥α,CE⊥α,且∠EBC=
,AB=6,AD⊥α,CE⊥α,且∠EBC=![]() ,AD=BE=8.求DE的长
,AD=BE=8.求DE的长
查看答案和解析>>
科目:高中数学 来源: 题型:
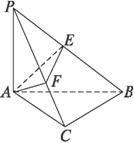
(1)求证:PB⊥平面AEF;
(2)若∠PBA=∠BAC=45°,求二面角A-PB-C的大小;
(3)若PA=AB=2,∠BPC=θ,求θ为何值时,S△AEF最大,最大值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com