已知函数f(x)=ex-ln(x+m)
(Ι)设x=0是f(x)的极值点,求m,并讨论f(x)的单调性;
(Ⅱ)当m≤2时,证明f(x)>0.
(Ⅰ)解:∵
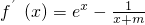
,x=0是f(x)的极值点,∴
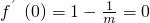
,解得m=1.
所以函数f(x)=e
x-ln(x+1),其定义域为(-1,+∞).
∵
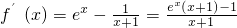
.
设g(x)=e
x(x+1)-1,则g
′(x)=e
x(x+1)+e
x>0,所以g(x)在(-1,+∞)上为增函数,
又∵g(0)=0,所以当x>0时,g(x)>0,即f
′(x)>0;当-1<x<0时,g(x)<0,f
′(x)<0.
所以f(x)在(-1,0)上为减函数;在(0,+∞)上为增函数;
(Ⅱ)证明:当m≤2,x∈(-m,+∞)时,ln(x+m)≤ln(x+2),故只需证明当m=2时f(x)>0.
当m=2时,函数
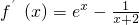
在(-2,+∞)上为增函数,且f
′(-1)<0,f
′(0)>0.
故f
′(x)=0在(-2,+∞)上有唯一实数根x
0,且x
0∈(-1,0).
当x∈(-2,x
0)时,f
′(x)<0,当x∈(x
0,+∞)时,f
′(x)>0,
从而当x=x
0时,f(x)取得最小值.
由f
′(x
0)=0,得
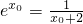
,ln(x
0+2)=-x
0.
故f(x)≥
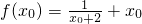
=
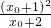
>0.
综上,当m≤2时,f(x)>0.
分析:(Ⅰ)求出原函数的导函数,因为x=0是函数f(x)的极值点,由极值点处的导数等于0求出m的值,代入函数解析式后再由导函数大于0和小于0求出原函数的单调区间;
(Ⅱ)证明当m≤2时,f(x)>0,转化为证明当m=0时f(x)>0.求出当m=2时函数的导函数,可知导函数在(-2,+∞)上为增函数,并进一步得到导函数在(-1,0)上有唯一零点x
0,则当x=x
0时函数取得最小值,借助于x
0是导函数的零点证出f(x
0)>0,从而结论得证.
点评:本题考查了利用导数研究函数的单调性,利用导数求函数在闭区间上的最值,考查了不等式的证明,考查了函数与方程思想,分类讨论的数学思想,综合考查了学生分析问题和解决问题的能力.熟练函数与导数的基础知识是解决该题的关键,是难题.

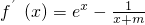 ,x=0是f(x)的极值点,∴
,x=0是f(x)的极值点,∴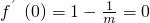 ,解得m=1.
,解得m=1.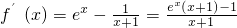 .
.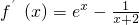 在(-2,+∞)上为增函数,且f′(-1)<0,f′(0)>0.
在(-2,+∞)上为增函数,且f′(-1)<0,f′(0)>0.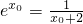 ,ln(x0+2)=-x0.
,ln(x0+2)=-x0.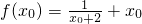 =
=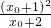 >0.
>0.
