
【题目】已知抛物线![]() 经过点
经过点![]() .
.
(1)写出抛物线![]() 的标准方程及其准线方程,并求抛物线
的标准方程及其准线方程,并求抛物线![]() 的焦点到准线的距离;
的焦点到准线的距离;
(2)过点![]() 且斜率存在的直线
且斜率存在的直线![]() 与抛物线
与抛物线![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,且点
,且点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(i)求点![]() 的坐标;
的坐标;
(ii)求![]() 与
与![]() 面积之和的最小值.
面积之和的最小值.
【答案】(1)![]() ,
,![]() ,焦点到准线的距离为1; (2)(i)
,焦点到准线的距离为1; (2)(i)![]() ,(ii)
,(ii)![]() .
.
【解析】
(1)由抛物线![]() 经过点
经过点![]() ,求得抛物线的方程为
,求得抛物线的方程为![]() ,再结合抛物线的几何性质,即可求解;
,再结合抛物线的几何性质,即可求解;
(2)(i)设过点![]() 的直线
的直线![]() ,联立方程组,求得
,联立方程组,求得![]() ,再由直线
,再由直线![]() 的方程,
的方程,![]() ,即可求解
,即可求解![]() 的坐标;
的坐标;
(ii)利用三角形的面积公式,求得![]() 与
与![]() 面积之和的表示,结合基本不等式,即可求解.
面积之和的表示,结合基本不等式,即可求解.
(1)由题意,抛物线![]() 经过点
经过点![]() ,即
,即![]() ,
,
解得![]() ,所以抛物线的方程为
,所以抛物线的方程为![]() ,
,
抛物线的准线方程为![]() ,抛物线的焦点到准线的距离为1.
,抛物线的焦点到准线的距离为1.
(2)(i)设过点![]() 的直线
的直线![]() ,
,
代入抛物线![]() 的方程,可得
的方程,可得![]() ,
,
设直线![]() 与抛物线
与抛物线![]() 的交点
的交点![]() ,且
,且![]() ,
,
则![]() ,
,
所以直线![]() 的方程为
的方程为![]() ,
,
即![]() ,即
,即![]() ,
,
令![]() ,可得
,可得![]() ,
,
所以![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
(ii)如图所示,可得![]() ,
,
![]() ,
,
所以![]() 与
与![]() 面积之和为:
面积之和为:

 ,
,
当且仅当![]() 时,即
时,即![]() 时等号成立,
时等号成立,
所以![]() 与
与![]() 面积之和的最小值为
面积之和的最小值为![]() .
.



科目:高中数学 来源: 题型:
【题目】设a,b,c为实数,f(x)=(x+a)(x2+bx+c),g(x)=(ax+1)(cx2+bx+1).记集合S={x|f(x)=0,x∈R},T={x|g(x)=0,x∈R}.若{S},{T}分别为集合S,T 的元素个数,则下列结论不可能的是( )
A.{S}=1且{T}=0B.{S}=1且{T}=1C.{S}=2且{T}=2D.{S}=2且{T}=3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了解广告投入对销售收益的影响,在若干地区各投入4万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示),由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.
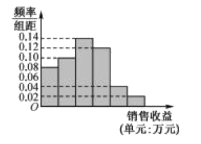
(1)根据频率分布直方图计算图中各小长方形的宽度;
(2)试估计该公司在若干地区各投入4万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
(3)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:
广告投入 | 1 | 2 | 3 | 4 | 5 |
销售收益 | 2 | 3 | 3 | 7 |
由表中的数据显示,![]() 与
与![]() 之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出
之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出![]() 关于
关于![]() 的回归直线方程.(参考公式:
的回归直线方程.(参考公式: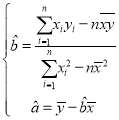 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年东京夏季奥运会将设置
年东京夏季奥运会将设置![]() 米男女混合泳接力这一新的比赛项目,比赛的规则是:每个参赛国家派出2男2女共计4名运动员比赛,按照仰泳
米男女混合泳接力这一新的比赛项目,比赛的规则是:每个参赛国家派出2男2女共计4名运动员比赛,按照仰泳![]() 蛙泳
蛙泳![]() 蝶泳
蝶泳![]() 自由泳的接力顺序,每种泳姿
自由泳的接力顺序,每种泳姿![]() 米且由一名运动员完成, 每个运动员都要出场. 现在中国队确定了备战该项目的4名运动员名单,其中女运动员甲只能承担仰泳或者自由泳,男运动员乙只能承担蝶泳或自由泳,剩下的男女各一名运动员则四种泳姿都可以上,那么中国队共有( )种兵布阵的方式.
米且由一名运动员完成, 每个运动员都要出场. 现在中国队确定了备战该项目的4名运动员名单,其中女运动员甲只能承担仰泳或者自由泳,男运动员乙只能承担蝶泳或自由泳,剩下的男女各一名运动员则四种泳姿都可以上,那么中国队共有( )种兵布阵的方式.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,我国自主研发的长征系列火箭的频频发射成功,标志着我国在该领域已逐步达到世界一流水平.火箭推进剂的质量为![]() ,去除推进剂后的火箭有效载荷质量为
,去除推进剂后的火箭有效载荷质量为![]() ,火箭的飞行速度为
,火箭的飞行速度为![]() ,初始速度为
,初始速度为![]() ,已知其关系式为齐奥尔科夫斯基公式:
,已知其关系式为齐奥尔科夫斯基公式:![]() ,其中
,其中![]() 是火箭发动机喷流相对火箭的速度,假设
是火箭发动机喷流相对火箭的速度,假设![]() ,
,![]() ,
,![]() ,
,![]() 是以
是以![]() 为底的自然对数,
为底的自然对数,![]() ,
,![]() .
.
(1)如果希望火箭飞行速度![]() 分别达到第一宇宙速度
分别达到第一宇宙速度![]() 、第二宇宙速度
、第二宇宙速度![]() 、第三宇宙速度
、第三宇宙速度![]() 时,求
时,求![]() 的值(精确到小数点后面1位).
的值(精确到小数点后面1位).
(2)如果希望![]() 达到
达到![]() ,但火箭起飞质量最大值为
,但火箭起飞质量最大值为![]() ,请问
,请问![]() 的最小值为多少(精确到小数点后面1位)?由此指出其实际意义.
的最小值为多少(精确到小数点后面1位)?由此指出其实际意义.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)若函数![]() 在
在![]() 处的切线平行于直线
处的切线平行于直线![]() ,求实数a的值;
,求实数a的值;
(Ⅱ)判断函数![]() 在区间
在区间![]() 上零点的个数;
上零点的个数;
(Ⅲ)在(Ⅰ)的条件下,若在![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
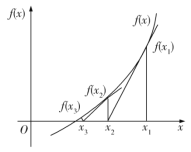
【题目】牛顿迭代法(Newton's method)又称牛顿–拉夫逊方法(Newton–Raphsonmethod),是牛顿在17世纪提出的一种近似求方程根的方法.如图,设![]() 是
是![]() 的根,选取
的根,选取![]() 作为
作为![]() 初始近似值,过点
初始近似值,过点![]() 作曲线
作曲线![]() 的切线
的切线![]() 与
与![]() 轴的交点的横坐标
轴的交点的横坐标![]() ,称
,称![]() 是
是![]() 的一次近似值,过点
的一次近似值,过点![]() 作曲线
作曲线![]() 的切线,则该切线与
的切线,则该切线与![]() 轴的交点的横坐标为
轴的交点的横坐标为![]() ,称
,称![]() 是
是![]() 的二次近似值.重复以上过程,直到
的二次近似值.重复以上过程,直到![]() 的近似值足够小,即把
的近似值足够小,即把![]() 作为
作为![]() 的近似解.设
的近似解.设![]() 构成数列
构成数列![]() .对于下列结论:
.对于下列结论:
①![]() ;
;
②![]() ;
;
③![]() ;
;
④![]() .
.
其中正确结论的序号为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 内有一点
内有一点![]() ,过
,过![]() 的两条直线
的两条直线![]() ,
,![]() 分别与抛物线
分别与抛物线![]() 交于
交于![]() ,
,![]() 和
和![]() ,
,![]() 两点,且满足
两点,且满足![]() ,
,![]() ,已知线段
,已知线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() .
.
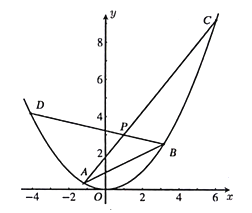
(1)求证:点![]() 的横坐标为定值;
的横坐标为定值;
(2)如果![]() ,点
,点![]() 的纵坐标小于3,求
的纵坐标小于3,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某产品1到6月份销售量及其价格进行调查,其售价x和销售量y之间的一组数据如下表所示:
月份i | 1 | 2 | 3 | 4 | 5 | 6 |
单价 | 9 | 9.5 | 10 | 10.5 | 11 | 8 |
销售量 | 11 | 10 | 8 | 6 | 5 | 14 |
(1)根据1至5月份的数据,求出y关于x的回归直线方程;
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过0.5元,则认为所得到的回归直线方程是理想的,试问所得到的回归直线方程是否理想?
(3)预计在今后的销售中,销售量与单价仍然服从(1)中的关系,且该产品的成本是2.5元/件,为获得最大利润,该产品的单价应定为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com