
| A�� | �٢� | B�� | �٢� | C�� | �٢ڢ� | D�� | �٢ڢ� |
���� �����жϺ���Ϊż�������ó����ۣ�
����|sinx|��1���ý��۳�����
�ۿ���ͨ��ͼ�������ֵ�ķ����жϣ�
�ܽ�Ϣ�һ����|kx|��|x|����|f��x��|��|x|������ֱ��y=kx���ҽ���һ�������㼴ԭ�㣮
��� �⣺�ٺ���y=f��x��Ϊż����������ͼ�����y��Գƣ�������Գ�ͼ�Σ�����ȷ��
�ڶ�����ʵ��x��|sinx|��1����|f��x��|��|x|������������ȷ��
�ۺ���y=f��x����ͼ����ֱ��y=x�������������㣬��������������ľ��벻һ����ȣ��ʴ���
�ܵ�����k����|k|��1ʱ��|kx|��|x|����|f��x��|��|x|������ֱ��y=kx���ҽ���һ�������㼴ԭ�㣬����ȷ��
�ʴ�ΪD��
���� �����˳����������ʺ�Ӧ�ã������ѶȽϴ�����ͣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �ɸĸ� | ���ɸĸ� | ����ν | |
| ��ʦ | 120 | y | 40 |
| ѧ�� | x | z | 130 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 Ϊ�˼��ij������ҵ��ѧ��������״�����Ӹð������ȡ��10λѧ�����г��أ���ͼΪ10λѧ�����صľ�Ҷͼ������ͼ����������ص�ʮλ���֣��ұ��Ǹ�λ���֣�����10λѧ�����ص�ƽ��������λ��֮��Ϊ����������������
Ϊ�˼��ij������ҵ��ѧ��������״�����Ӹð������ȡ��10λѧ�����г��أ���ͼΪ10λѧ�����صľ�Ҷͼ������ͼ����������ص�ʮλ���֣��ұ��Ǹ�λ���֣�����10λѧ�����ص�ƽ��������λ��֮��Ϊ����������������| A�� | 0.1 | B�� | 0.2 | C�� | 0.3 | D�� | 0.4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x2+y2+2x+3y+5=0 | B�� | x2+y2+2x+3y+6=0 | C�� | x2+y2+2x+3y+3=0 | D�� | x2+y2+2x+3y+4=0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
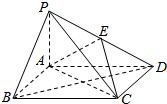 ��ͼ������P-ABCD�У�����ABCDΪƽ���ı��Σ�AP=1��AD=$\sqrt{3}$��PA��ƽ��ABCD��EΪPD���е㣮
��ͼ������P-ABCD�У�����ABCDΪƽ���ı��Σ�AP=1��AD=$\sqrt{3}$��PA��ƽ��ABCD��EΪPD���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �ڶ�����ABCDEF�У�����ABCD�����Σ��ı���ADEF�������Σ�AB��DC��AB=AD=1��CD=2��AC=EC=$\sqrt{5}$��
�ڶ�����ABCDEF�У�����ABCD�����Σ��ı���ADEF�������Σ�AB��DC��AB=AD=1��CD=2��AC=EC=$\sqrt{5}$���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com