
分析 因为函数f(x)和g(x)都没给出解析式,所以求解g(2002)只能依靠f(1),由g(x)=f(x)+1-x可求出g(1),问题变成了求函数g(x)的周期问题,先把g(x)=f(x)+1-x变形得到g(x)+x-1=f(x),然后把x+5和x+1两次代入此式,借助于f(x+5)≥f(x)+5与f(x+1)≤f(x)+1变换得到函数g(x)的周期,则问题可求.
解答 解:由g(x)=f(x)+1-x得g(x)+x-1=f(x)
∴g(x+5)+(x+5)-1=f(x+5)≥f(x)+5=g(x)+(x-1)+5
g(x+1)+(x+1)-1=f(x+1)≤f(x)+1=g(x)+(x-1)+1
∴g(x+5)≥g(x),g(x+1)≤g(x)
∴g(x)≤g(x+5)≤g(x+4)≤g(x+3)≤g(x+2)≤g(x+1)
∴g(x+1)=g(x)
∴T=1
∵g(1)=f(1)+1-1=1
∴g(2015)=1
故答案为:1.
点评 本题考查了函数的周期性,训练了抽象函数的灵活代换和变换方法,解答此题的关键在于一个“变”字,考查了学生的应变能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${a_n}=\frac{n}{n+1}({n∈{N^*}})$ | B. | ${a_n}={n^2}-1({n∈{N^*}})$ | ||
| C. | ${a_n}=5n+{({-1})^n}({n∈{N^*}})$ | D. | ${a_n}=3n-1({n∈{N^*}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
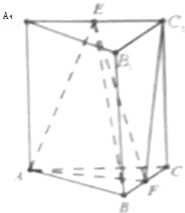 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,E,F分别为A1C1,BC的中点,AA1=3,AC=2,BC=1,AB⊥BC.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,E,F分别为A1C1,BC的中点,AA1=3,AC=2,BC=1,AB⊥BC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A0与A2 | B. | A1与A2 | C. | A1与A3 | D. | A0与A3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com