
科目:高中数学 来源:2014-2015学年天津市高三上学期第二次月考文科数学试卷(解析版) 题型:填空题
家政服务公司根据用户满意程度将本公司家政服务员分为两类,其中A类服务员12名,B类服务员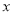 名
名
(Ⅰ)若采用分层抽样的方法随机抽取20名家政服务员参加技术培训,抽取到B类服务员的人数是16,求 的值
的值
(Ⅱ)某客户来公司聘请2名家政服务员,但是由于公司人员安排已经接近饱和,只有3名A类家政服务员和2名B类家政服务员可供选择
①请列出该客户的所有可能选择的情况
②求该客户最终聘请的家政服务员中既有A类又有B类的概率
查看答案和解析>>
科目:高中数学 来源:2014-2015学年天津市南开区高三一模文科数学试卷(解析版) 题型:解答题
(本小题满分13分)设数列{an}满足:a1=1,an+1=3an,n∈N*.设Sn为数列{bn}的前n项和,已知b1≠0,2bn–b1=S1Sn,n∈N*.
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)设cn=bnlog3an,求数列{cn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年天津市南开区高三一模理科数学试卷(解析版) 题型:填空题
已知正三角形ABC的边长为2,点D,E分别在边AB,AC上,且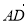 =
= 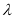
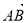 ,
,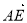 =
= 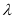
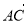 .若点F为线段BE的中点,点O为△ADE的重心,则
.若点F为线段BE的中点,点O为△ADE的重心,则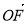
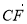 = .
= .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省资阳市高三第三次模拟考试文科数学试卷(解析版) 题型:解答题
(本小题满分12分)已知数列{an},{bn}满足:a1b1+a2b2+a3b3+…+anbn=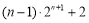 (
(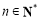 ).
).
(Ⅰ)若{bn }是首项为1,公比为2等比数列,求数列{an}的通项公式;
(Ⅱ)在数列{an}中,a1=1,对任意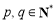 ,
,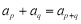 ,记数列{an+bn}的前n项和为Tn,求满足不等式
,记数列{an+bn}的前n项和为Tn,求满足不等式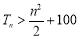 的自然数n的最小值.
的自然数n的最小值.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年新疆乌鲁木齐高三第一次诊断性测验文科数学卷(解析版) 题型:解答题
(本题满分10分)选修4-1:几何证明选讲
过以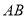 为直径的圆上
为直径的圆上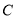 点作直线交圆于
点作直线交圆于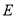 点,交
点,交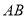 挺长线于
挺长线于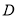 点,过
点,过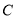 点作圆的切线交
点作圆的切线交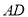 于
于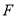 点,交
点,交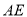 挺长线于
挺长线于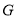 点,且
点,且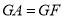 。
。
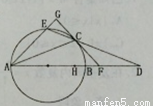
(Ⅰ)求证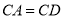 ;
;
(Ⅱ)设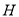 为
为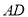 的中点,求证
的中点,求证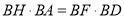
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com