
分析 (1)通过-x代替x,推出方程,求解函数g(x)的解析式.利用h(x)是二次函数,且h(-2)=h(0)=1,可设h(x)=ax(x+2)+1,然后求解即可.
(2)设ϕ(x)=h(x)+ax+5=-x2+(a-2)x+6,F(x)=ex-3-x(ex-3)=(1-x)ex+3x-3,转化条件为当-1≤x≤1时,ϕ(x)min≥F(x)max,通过函数的导数求解函数的最值,列出关系式即可求出实数a的取值范围.
(3)设t=a+5,由(2)知,画出函数在2≤t≤12f(x)的图象,设f(x)=T,则f(T)=t当t=2,当2<t<e2-3,当t=e2-3,当e2-3<t≤12,分别判断函数的图象交点个数,得到结论.
解答  解:(1)∵$g(x)+2g(-x)={e^x}+\frac{2}{e^x}-9$,①$g(-x)+2g(x)={e^{-x}}+\frac{2}{{{e^{-x}}}}-9$,即$g(-x)+2g(x)=2{e^x}+\frac{1}{e^x}-9$,②
解:(1)∵$g(x)+2g(-x)={e^x}+\frac{2}{e^x}-9$,①$g(-x)+2g(x)={e^{-x}}+\frac{2}{{{e^{-x}}}}-9$,即$g(-x)+2g(x)=2{e^x}+\frac{1}{e^x}-9$,②
由①②联立解得:g(x)=ex-3.…(2分)
∵h(x)是二次函数,且h(-2)=h(0)=1,可设h(x)=ax(x+2)+1,
由h(-3)=-2,解得a=-1.
∴h(x)=-x(x+2)+1=-x2-2x+1
∴g(x)=ex-3,h(x)=-x2-2x+1.…(4分)
(2)设ϕ(x)=h(x)+ax+5=-x2+(a-2)x+6,F(x)=ex-3-x(ex-3)=(1-x)ex+3x-3,
依题意知:当-1≤x≤1时,ϕ(x)min≥F(x)max
∵F'(x)=-ex+(1-x)(ex-3)+3=-xex+3,在[-1,1]上单调递减,
∴F'(x)min=F'(1)=3-e>0…(6分)
∴F(x)在[-1,1]上单调递增,∴F(x)max=F(1)=0
∴$\left\{\begin{array}{l}ϕ({-1})=7-a≥0\\ ϕ(1)=a+3≥0\end{array}\right.$,解得:-3≤a≤7
∴实数a的取值范围为[-3,7].…(8分)
(3)设t=a+5,由(Ⅱ)知,2≤t≤12f(x)的图象如图所示:
设f(x)=T,则f(T)=t
当t=2,即a=-3时,T1=-1,T2=ln5,f(x)=-1有两个 解,f(x)=ln5有3个解;
当2<t<e2-3,即-3<a<e2-8时,T=ln(t+3)且ln5<T<2,f(x)=T有3个解;
当t=e2-3,即a=e2-8时,T=2,f(x)=T有2个解;
当e2-3<t≤12,即e2-8<a≤7时,T=ln(t+3)>2,f(x)=T有1个解.
综上所述:
当a=-3时,方程有5个解;
当-3<a<e2-8时,方程有3个解.…(12分)
点评 本题考查函数恒成立,二次函数的性质,函数的导数的综合应用,函数的图象以及函数的零点个数的求法,考查分类讨论思想数形结合思想以及转化思想的应用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
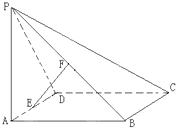 如图:四棱锥P-ABCD的底面是平行四边形,∠DAB=60°,平面PAB⊥ABD,
如图:四棱锥P-ABCD的底面是平行四边形,∠DAB=60°,平面PAB⊥ABD,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
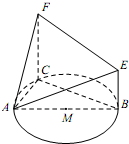 如图,某简单几何体的一个面ABC内接于圆M,AB是圆M的直径,CF∥BE,BE⊥平面ABC,且AB=2,AC=1,BE+CF=7.
如图,某简单几何体的一个面ABC内接于圆M,AB是圆M的直径,CF∥BE,BE⊥平面ABC,且AB=2,AC=1,BE+CF=7.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com