
分析 由题意可得∫${\;}_{-1}^{1}$($\sqrt{1{-x}^{2}}$+x3)dx=∫${\;}_{-1}^{1}$$\sqrt{1{-x}^{2}}$dx+∫${\;}_{-1}^{1}$x3dx,分别由定积分的几何意义和牛顿-莱布尼兹公式可得.
解答 解:∫${\;}_{-1}^{1}$($\sqrt{1{-x}^{2}}$+x3)dx=∫${\;}_{-1}^{1}$$\sqrt{1{-x}^{2}}$dx+∫${\;}_{-1}^{1}$x3dx,
∵∫${\;}_{-1}^{1}$$\sqrt{1{-x}^{2}}$dx表示单位圆x2+y2=1的上半个圆的面积,
∴∫${\;}_{-1}^{1}$$\sqrt{1{-x}^{2}}$dx=$\frac{π}{2}$,又∫${\;}_{-1}^{1}$x3dx=$\frac{1}{4}$x4${|}_{-1}^{1}$=0,
∴∫${\;}_{-1}^{1}$($\sqrt{1{-x}^{2}}$+x3)dx=$\frac{π}{2}$,
故答案为:$\frac{π}{2}$.
点评 本题考查定积分的求解,涉及定积分的几何意义和公式求解,属基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
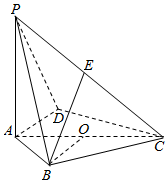 如图,在四棱锥P-ABCD中,底面四边形ABCD内接于圆O,AC是圆O的一条直径,PA⊥平面ABCD,PA=AC=2,E是PC的中点,∠DAC=∠AOB
如图,在四棱锥P-ABCD中,底面四边形ABCD内接于圆O,AC是圆O的一条直径,PA⊥平面ABCD,PA=AC=2,E是PC的中点,∠DAC=∠AOB查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{π}{3}$,$\frac{π}{2}$) | B. | [$\frac{2π}{3}$,π) | C. | [0,$\frac{π}{2}$)∪($\frac{π}{2}$,$\frac{2π}{3}$] | D. | [0,$\frac{π}{2}$)∪[$\frac{2π}{3}$,π) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移3,向上平移1个单位 | B. | 向右平移3,向上平移1个单位 | ||
| C. | 向左平移3,向下平移1个单位 | D. | 向右平移3,向下平移1个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥S-ABCD的底面是正方形,SA⊥底面ABCD,E是SC中点,SA=4,AB=2.
如图,四棱锥S-ABCD的底面是正方形,SA⊥底面ABCD,E是SC中点,SA=4,AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com