
【题目】已知函数![]() ,且
,且![]() .
.
(1)求函数![]() 的极值;
的极值;
(2)当![]() 时,证明:
时,证明:![]() .
.
【答案】(1)![]() 有极大值
有极大值![]() ,函数
,函数![]() 有极小值
有极小值![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析:(1)求极值,可先求得导数![]() ,然后通过解不等式
,然后通过解不等式![]() 确定增区间,解不等式
确定增区间,解不等式![]() 确定减区间,则可得极大值和极小值;(2)要证明此不等式,我们首先研究不等式左边的函数,记
确定减区间,则可得极大值和极小值;(2)要证明此不等式,我们首先研究不等式左边的函数,记![]() ,求出其导数
,求出其导数![]() ,可知
,可知![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,![]() ,这是
,这是![]() 时最小值,
时最小值,![]() ,这是
,这是![]() 时的最大值,因此要证明题中不等式,可分类,
时的最大值,因此要证明题中不等式,可分类,![]() 和
和![]() 分别证明.
分别证明.
试题解析:(1)依题意,![]() ,
,
故![]() ,
,
令![]() ,则
,则![]() 或
或![]() ; 令
; 令![]() ,则
,则![]() ,
,
故当![]() 时,函数
时,函数![]() 有极大值
有极大值![]() ,当
,当![]() 时,函数
时,函数![]() 有极小值
有极小值![]() .
.
(2) 由(1)知![]() ,令
,令![]() ,
,
则![]() ,
,
可知![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,令
上单调递减,令![]() .
.
① 当![]() 时,
时,![]() ,所以函数
,所以函数![]() 的图象在
的图象在![]() 图象的上方.
图象的上方.
② 当![]() 时,函数
时,函数![]() 单调递减,所以其最小值为
单调递减,所以其最小值为![]() 最大值为2,而
最大值为2,而![]() ,所以函数
,所以函数![]() 的图象也在
的图象也在![]() 图象的上方.
图象的上方.
综上可知,当![]() 时,
时,![]()


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:
【题目】对于在区间[m,n]上有意义的两个函数f(x)与g(x),如果对任意x∈[m,n]均有|f(x)﹣g(x)|≤1,则称f(x)与g(x)在[m,n]上是接近的;否则称f(x)与g(x)在[m,n]上是非接近的.现有两个函数f1(x)=loga(x﹣3a),与f2(x)=loga ![]() (a>0,a≠1),给定区间[a+2,a+3].
(a>0,a≠1),给定区间[a+2,a+3].
(1)若f1(x)与f1(x)在给定区间[a+2,a+3]上都有意义,求a的取值范围;
(2)讨论f1(x)与f1(x)在给定区间[a+2,a+3]上是否是接近的?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)某企业生产的一批产品中有一、二、三等品及次品共四个等级,1件不同等级产品的利润(单位:元)如表1,从这批产品中随机抽取出1件产品,该件产品为不同等级的概率如表2.
等级 | 一等品 | 二等品 | 三等品 | 次品 |
|
| |
|
|
等级 | 一等品 | 二等品 | 三等品 | 次品 |
利润 | |
|
|
|
表1 表2
若从这批产品中随机抽取出的1件产品的平均利润(即数学期望)为![]() 元.
元.
(1) 设随机抽取1件产品的利润为随机变量![]() ,写出
,写出![]() 的分布列并求出
的分布列并求出![]() 的值;
的值;
(2) 从这批产品中随机取出3件产品,求这3件产品的总利润不低于17元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若![]() ,求函数
,求函数![]() 的图象在
的图象在![]() 处的切线方程;
处的切线方程;
(2)若![]() ,试讨论方程
,试讨论方程![]() 的实数解的个数;
的实数解的个数;
(3)当![]() 时,若对于任意的
时,若对于任意的![]() ,都存在
,都存在![]() ,使得
,使得![]() ,求满足条件的正整数
,求满足条件的正整数![]() 的取值的集合.
的取值的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥S﹣ABC中,∠SBA=∠SCA=90°,△ABC是斜边AB=a的等腰直角三角形,则以下结论中: ①异面直线SB与AC所成的角为90°;
②直线SB⊥平面ABC;
③面SBC⊥面SAC;
④点C到平面SAB的距离是 ![]() .
.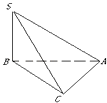
其中正确结论的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查观众对某电视剧的喜爱程度,某电视台在甲乙两地随机抽取了8名观众做问卷调查,得分结果如图所示:
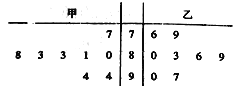
(1)计算甲地被抽取的观众问卷得分的中位数和乙地被抽取的观众问卷得分的平均数;
(2)用频率估计概率,若从乙地的所有观众中再随机抽取4人进行问卷调查,记问卷分数不低于80分的人数为![]() ,求
,求![]() 的分布列与期望.
的分布列与期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}中a2=2,a5= ![]() ,则a1a2+a2a3+a3a4+…+anan+1等于( )
,则a1a2+a2a3+a3a4+…+anan+1等于( )
A.16(1﹣4﹣n)
B.16(1﹣2n)
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com