
【题目】已知函数![]() 。
。
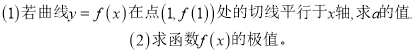
【答案】(1) ![]() (2)
(2) 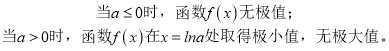
【解析】试题分析:
(1)首先求得函数的导函数,然后结合切线与导数的关系得到关于实数a的方程,解方程可得a=e;
(2)结合导函数的解析式与函数极值的关系分类讨论可得:当a≤0时,函数f(x)无极值,当a>0时,函数f(x)在x=lna处取得极小值,无极大值.
试题解析:
由f(x)=x-1+![]() 且其定义域为R
且其定义域为R
(1)曲线y=f(x)在(1,f(1))处切线平行于x轴,则f' (1)=0即![]()
(2)由f' (x)=1-![]() 且其定义域为R
且其定义域为R
①.当a≤0时f' (x)>0在R上恒成立,f(x)在(-∞,+∞)上单调递增,故f(x)无极值
②当a>0时,f' (x)= ![]() 由f' (x)>0得x>lna,由f' (x)<0得x<lna,
由f' (x)>0得x>lna,由f' (x)<0得x<lna,
即f(x)在(-∞,lna)单调递减,(lna,+∞)单调递增.
故f(x)在(-∞,+∞)上x=lna处取得极小值,f(lna)=lna无极大值.
综上所述:当a≤0时,函数f(x)无极值,当a>0时,函数f(x)在x=lna处取得极小值,无极大值.


科目:高中数学 来源: 题型:
【题目】已知a、b∈R,向量 ![]() =(x , 1),
=(x , 1), ![]() =(﹣1,b﹣x),函数f(x)=a﹣
=(﹣1,b﹣x),函数f(x)=a﹣ ![]() 是偶函数.
是偶函数.
(1)求b的值;
(2)若在函数定义域内总存在区间[m,n](m<n),使得y=f(x)在区间[m,n]上的函数值组成的集合也是[m,n],求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点,动点
的左、右焦点,动点![]() 在
在![]() 上,连结
上,连结![]() 并延长
并延长![]() 至
至![]() 点,使得
点,使得![]() ,设点
,设点![]() 的轨迹为
的轨迹为![]() .
.
(1)求![]() 的方程;
的方程;
(2)设![]() 为坐标原点,点
为坐标原点,点![]() ,连结
,连结![]() 交
交![]() 于
于![]() 点,若直线
点,若直线![]() 的斜率与直线
的斜率与直线![]() 的斜率存在且不为零,证明: 这两条直线的斜率之比为定值.
的斜率存在且不为零,证明: 这两条直线的斜率之比为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线y=x3+x-2在点P0处的切线l1平行于直线4x-y-1=0,且点P0在第三象限.
(1)求P0的坐标;(2)若直线l⊥l1,且l也过切点P0,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=3|x|+log3|x|.
(1)判断函数的奇偶性,并加以证明;
(2)说明函数f(x)在(0,+∞)上的单调性,并利用单调性定义证明;
(3)若 f(2a)<28,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)
已知函数f(x)=(x2+bx+b)![]() (b∈R).
(b∈R).
(1)当b=4时,求f(x)的极值;
(2)若f(x)在区间![]() 上单调递增,求b的取值范围.
上单调递增,求b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com