
【题目】(本小题满分10分)
已知函数f(x)=(x2+bx+b)![]() (b∈R).
(b∈R).
(1)当b=4时,求f(x)的极值;
(2)若f(x)在区间![]() 上单调递增,求b的取值范围.
上单调递增,求b的取值范围.
【答案】(1) 4;(2)![]() .
.
【解析】试题分析:(1)把![]() 代入函数的解析式,求出函数的导函数,由导函数的零点对定义域分段,由导函数在各区间段内的符号判断原函数的单调性,从而求得极值;(2)由函数的解析式,求出函数的导函数,由自变量的取值范围本题可转化为
代入函数的解析式,求出函数的导函数,由导函数的零点对定义域分段,由导函数在各区间段内的符号判断原函数的单调性,从而求得极值;(2)由函数的解析式,求出函数的导函数,由自变量的取值范围本题可转化为![]() 可求得
可求得![]() 的值.
的值.
(1)当b=4时,f′(x)=![]() ,
,
由f′(x)=0得x=-2或x=0.
当x∈(-∞,-2)时,f′(x)<0,f(x)单调递减;
当x∈(-2,0)时,f′(x)>0,f(x)单调递增;
当x∈![]() 时,f′(x)<0,f(x)单调递减,故f(x)在x=-2取极小值f(-2)=0,在x=0取极大值f(0)=4.
时,f′(x)<0,f(x)单调递减,故f(x)在x=-2取极小值f(-2)=0,在x=0取极大值f(0)=4.
(2)f′(x)=![]() ,
,
因为当x∈![]() 时,
时,![]() <0,
<0,
依题意当x∈![]() 时,有5x+(3b-2)≤0,从而
时,有5x+(3b-2)≤0,从而![]() +(3b-2)≤0.
+(3b-2)≤0.
所以b的取值范围为![]()


科目:高中数学 来源: 题型:
【题目】三棱锥S﹣ABC中,∠SBA=∠SCA=90°,△ABC是斜边AB=a的等腰直角三角形,则以下结论中: ①异面直线SB与AC所成的角为90°;
②直线SB⊥平面ABC;
③面SBC⊥面SAC;
④点C到平面SAB的距离是 ![]() .
.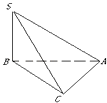
其中正确结论的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查观众对某电视剧的喜爱程度,某电视台在甲乙两地随机抽取了8名观众做问卷调查,得分结果如图所示:
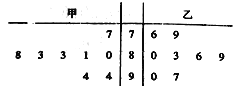
(1)计算甲地被抽取的观众问卷得分的中位数和乙地被抽取的观众问卷得分的平均数;
(2)用频率估计概率,若从乙地的所有观众中再随机抽取4人进行问卷调查,记问卷分数不低于80分的人数为![]() ,求
,求![]() 的分布列与期望.
的分布列与期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的圆台中,AC是下底面圆O的直径,EF是上底面圆O′的直径,FB是圆台的一条母线.
(I)已知G,H分别为EC,FB的中点,求证:GH∥平面ABC;
(Ⅱ)已知EF=FB= ![]() AC=2
AC=2 ![]() ,AB=BC,求二面角F﹣BC﹣A的余弦值.
,AB=BC,求二面角F﹣BC﹣A的余弦值.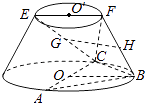
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过直线x=﹣2上的动点P作抛物线y2=4x的两条切线PA,PB,其中A,B为切点.
(1)若切线PA,PB的斜率分别为k1 , k2 , 求证:k1k2为定值;
(2)求证:直线AB恒过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}中a2=2,a5= ![]() ,则a1a2+a2a3+a3a4+…+anan+1等于( )
,则a1a2+a2a3+a3a4+…+anan+1等于( )
A.16(1﹣4﹣n)
B.16(1﹣2n)
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别是角A,B,C的对边,且2cosAcosC(1-tanAtanC)=1.
(1)求B的大小;
(2)若b=![]() ,求△ABC面积的最大值.
,求△ABC面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com