
分析 首项分别求出AQ,AP,PQ,利用余弦定理求∠PAQ.
解答 解:在边长为3的正方形ABCD中,点P,Q分别在边CD、BC上,满足DP=1,CQ=QB.
所以$A{Q}^{2}=A{B}^{2}+B{Q}^{2}=\frac{45}{4}$,AP2=AD2+PD2=10,$P{Q}^{2}=P{C}^{2}+Q{C}^{2}=\frac{25}{4}$,
由余弦定理得到cos∠PAQ=$\frac{A{Q}^{2}+A{P}^{2}-P{Q}^{2}}{2AQ•AP}$=$\frac{15}{2\sqrt{\frac{45}{4}}\sqrt{10}}=\frac{\sqrt{2}}{2}$,所以∠PAQ=$\frac{π}{4}$;
故答案为:$\frac{π}{4}$.
点评 本题考查了余弦定理的运用求三角形的内角;熟练掌握余弦定理是解答的关键.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2]∪(-1,$\frac{3}{2}$) | B. | (-∞,-2]∪(-1,-$\frac{3}{4}$) | C. | (-∞,$\frac{1}{4}$)∪($\frac{1}{4}$,+∞) | D. | (-1,-$\frac{3}{4}$)∪[$\frac{1}{4}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
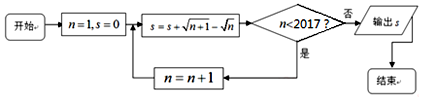
| A. | $\sqrt{2018}-1$ | B. | $\sqrt{2017}-1$ | C. | $\sqrt{2016}-1$ | D. | $\sqrt{2015}-1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 积极锻炼身体 | 不积极锻炼身体 | 合计 | |
| 健康状况良好 | 18 | 7 | 25 |
| 健康状况一般 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
| P(k2>k) | 0.15 | 0.10 | 0.06 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com