
【题目】如图,从2009年参加奥运知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如图所示.观察图形,估计这次奥运知识竞赛的及格率(大于或等于60分为及格)为 . 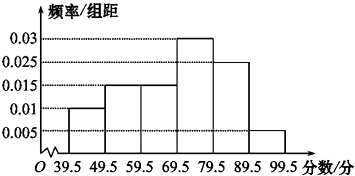
【答案】75%
【解析】解:大于或等于60分的共四组,它们是:
[59.5,69.5),[69.5,79.5),[79.5,89.5),[89.5,99.5).
分别计算出这四组的频率,
如[79.5,89.5)这一组的矩形的高为0.025
直方图中的各个矩形的面积代表了频率,则[79.5,89.5)这一组的频率=0.025×10=0.25
同样可得,60分及以上的频率=(0.015+0.03+0.025+0.005)×10=0.75
估计这次奥运知识竞赛的及格率(大于或等于60分为及格)为75%,
所以答案是:75%.
【考点精析】通过灵活运用频率分布直方图和用样本的频率分布估计总体分布,掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息;样本数据的频率分布表和频率分布直方图,是通过各小组数据在样本容量中所占比例大小来表示数据的分布规律,它可以让我们更清楚的看到整个样本数据的频率分布情况,并由此估计总体的分布情况即可以解答此题.


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,直线![]() 的参数方程为
的参数方程为 (其中t为参数).现以坐标原点为极点,
(其中t为参数).现以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() .
.
(Ⅰ) 写出直线![]() 的普通方程和曲线C 的直角坐标方程;
的普通方程和曲线C 的直角坐标方程;
(Ⅱ) 过点![]() 且与直线
且与直线![]() 平行的直线
平行的直线![]() 交曲线C于
交曲线C于![]() ,
, ![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设b和c分别是先后抛掷一枚骰子得到的点数,用随机变量ξ表示方程x2+bx+c=0实根的个数(重根按一个计).
(1)求方程x2+bx+c=0有实根的概率;
(2)求ξ的分布列和数学期望;
(3)求在先后两次出现的点数中有5的条件下,方程x2+bx+c=0有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (x+
(x+ ![]() ),g(x)=
),g(x)= ![]() (x﹣
(x﹣ ![]() ).
).
(1)求函数h(x)=f(x)+2g(x)的零点;
(2)求函数F(x)=[f(x)]2n﹣[g(x)]2n(n∈N*)的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三个顶点坐标分别为A(﹣1,1),B(7,﹣1),C(﹣2,5),AB边上的中线所在直线为l.
(1)求直线l的方程;
(2)若点A关于直线l的对称点为D,求△BCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com