已知等比数列{an}中,a2=2,a5=128,若bn=log2an,数列{bn}前n项的和为Sn.
(Ⅰ)求数列{bn}的前n项和Sn;
(Ⅱ)求不等式Sn<2bn的解集.
解:(I)在等比数列{a
n}中,由a
5=a
2q
3,又a
2=2,a
5=128,q
3=64,
∴q=4,∴a
n=a
2q
n-2=2•4
n-2=2
2n-3,
∴b
n=log
2a
n=log
22
2n-3=2n-3.b
n=b
1+b
2+b
3+…+b
n=(2•1-3)+(2•2-3)+(2•3-3)+…+(2•n-3)
=2(1+2+3+…+n)-3n=n
2-2n
(II)由S
n<2b
n,得n
2-2n<2(2n-3),即n
2-6n+6<0,
∴
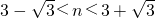
又n∈N
*,
∴n=2,3,4
故原不等式的解集是{2,3,4}
分析:(I)设数列{a
n}的公比为q,由a
2=2,a
5=128求得a
1和q,再根据等比数列{a
n}的通项公式,进而可知数列{b
n}是等差数列.再利用等差数列的求和公式求得答案.
(II)由S
n<2b
n,得n
2-2n<2(2n-3),即n
2-6n+6<0,解不等式即可
点评:本题主要考查了等比数列的通项公式及不等式的解法.属基础题.

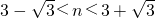 又n∈N*,
又n∈N*,

 阅读快车系列答案
阅读快车系列答案