
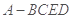 的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.
的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.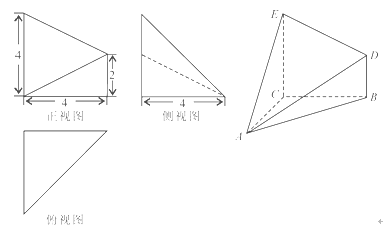
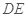 与
与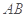 所成角的余弦值;
所成角的余弦值;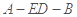 的正弦值;
的正弦值; 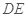 与
与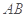 所成的角的余弦值为
所成的角的余弦值为 .
. 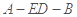 的的正弦值为
的的正弦值为 .
.  ,通过取
,通过取 的中点
的中点 ,连结
,连结 ,
, ,∴
,∴ 或其补角即为异面直线
或其补角即为异面直线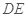 与
与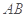 所成的角. 在
所成的角. 在 中即可解得
中即可解得 的余弦值.
的余弦值.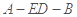 的棱为
的棱为 ,可通过三垂线法找二面角,由已知
,可通过三垂线法找二面角,由已知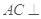 平面
平面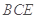 ,过
,过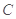 作
作 交
交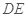 于
于 ,连
,连 .可得
.可得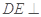 平面
平面 ,从而
,从而 ,∴
,∴ 为二面角
为二面角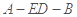 的平面角. 在
的平面角. 在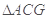 中可解得
中可解得 角的正弦值.
角的正弦值.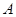 为顶点,
为顶点,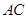 为高的,
为高的,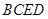 为底的四棱锥,所以
为底的四棱锥,所以
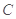 为原点,以
为原点,以 所在直线为
所在直线为 轴建立空间直角坐标系来解答.
轴建立空间直角坐标系来解答. 的中点是
的中点是 ,连结
,连结 ,
, ,∴
,∴ 或其补角即为异面直线
或其补角即为异面直线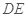 与
与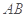 所成的角.
所成的角.  中,
中, ,
, .∴
.∴ .
. 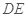 与
与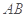 所成的角的余弦值为
所成的角的余弦值为 .
. 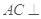 平面
平面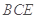 ,过
,过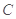 作
作 交
交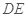 于
于 ,连
,连 .
.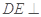 平面
平面 ,从而
,从而 ,
, 为二面角
为二面角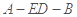 的平面角.
的平面角. 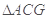 中,
中,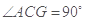 ,
, ,
, ,
, .∴
.∴ .
.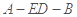 的的正弦值为
的的正弦值为 .
.  ,∴几何体的体积为16.
,∴几何体的体积为16. 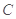 为原点,以CA,CB,CE所在直线为x,y,z轴建立空间直角坐标系.
为原点,以CA,CB,CE所在直线为x,y,z轴建立空间直角坐标系.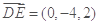 ,
,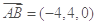 ,∴
,∴ ,
,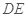 与
与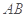 所成的角的余弦值为
所成的角的余弦值为 .
. 的一个法向量为
的一个法向量为 ,设平面ADE的一个法向量为
,设平面ADE的一个法向量为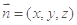 ,
, ,
,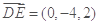 ,
, , ∴
, ∴
 ,
, ,
,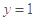 ,则
,则 ,
,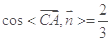 ,
,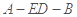 的的正弦值为
的的正弦值为 .
.  ,∴几何体的体积为16.
,∴几何体的体积为16.

科目:高中数学 来源:不详 题型:单选题
 A1B1C1D1中, P,Q是面对角线A1C1上的两个不同动点.
A1B1C1D1中, P,Q是面对角线A1C1上的两个不同动点.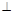 DQ;
DQ;| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.有两个面平行,其余各面都是四边形的几何体叫棱柱. |
| B.有两个面平行,其余各面都是平行四边形的几何体叫棱柱. |
| C.有两个面平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行的几何体叫棱柱. |
| D.用一个平面去截棱锥,底面与截面之间的部分组成的几何体叫棱台. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
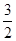 ,EF与面AC的距离为2,则该多面体的体积为____________.
,EF与面AC的距离为2,则该多面体的体积为____________.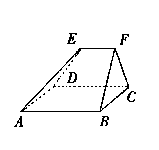
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
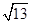 ,AB⊥平面ACD,则四面体 ABCD外接球的表面积为( )
,AB⊥平面ACD,则四面体 ABCD外接球的表面积为( )| A.36π | B.88π | C.92π | D.128π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com