已知数列{an}的前n项和Sn=kcn-k(其中c,k为常数),且a2=4,a6=8a3.
(1)求an;
(2)求数列{nan}的前n项和Tn.
解:(1)由S
n=kc
n-k,得a
n=s
n-s
n-1=kc
n-kc
n-1; (n≥2),
由a
2=4,a
6=8a
3.得kc(c-1)=4,kc
5(c-1)=8kc
2(c-1),解得
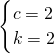
;
所以a
1=s
1=2;
a
n=s
n-s
n-1=kc
n-kc
n-1=2
n,(n≥2),
于是a
n=2
n.
(2):∵na
n=n•2
n;
∴T
n=2+2•2
2+3•2
3+…+n•2
n;
2T
n=2
2+2•2
3+3•2
4+…+(n-1)•2
n+n•2
n+1;
∴-T
n=2+2
2+2
3…+2
n-n•2
n+1=
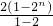
-n•2
n+1=-2+2
n+1-n•2
n+1;
即:T
n=(n-1)•2
n+1+2.
分析:(1)先根据前n项和求出数列的通项表达式;再结合a
2=4,a
6=8a
3求出c,k,即可求出数列的通项;
(2)直接利用错位相减法求和即可.
点评:本题主要考察数列求和的错位相减法.数列求和的错位相减法适用于一等差数列乘一等比数列组合而成的新数列.数列求和的错位相减法也是这几年高考的常考点.

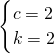 ;
;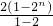 -n•2n+1=-2+2n+1-n•2n+1;
-n•2n+1=-2+2n+1-n•2n+1;
