
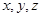 分别表示甲,乙,丙3个盒中的球数.
分别表示甲,乙,丙3个盒中的球数.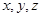 依次成公差大于0的等差数列的概率;
依次成公差大于0的等差数列的概率;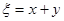 ,求随机变量
,求随机变量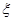 的概率分布列和数学期望.
的概率分布列和数学期望. 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:解答题
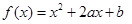
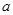 是从
是从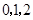 三个数中任取的一个数,
三个数中任取的一个数,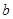 是从
是从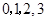 四个数中任取的一个数,求
四个数中任取的一个数,求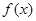 为偶函数的概率;
为偶函数的概率;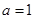 ,
,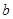 是从区间
是从区间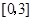 任取的一个数,求方程
任取的一个数,求方程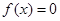 有实根的概率.
有实根的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,乙队每人答对的概率都是
,乙队每人答对的概率都是 .设每人回答正确与否相互之间没有影响,用
.设每人回答正确与否相互之间没有影响,用 表示甲队总得分.
表示甲队总得分. 的分布列及其数学期望E(
的分布列及其数学期望E( );
);查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
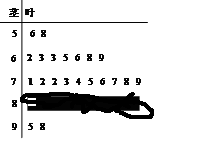

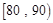 之间的频数,并计算频率分布直方图中
之间的频数,并计算频率分布直方图中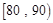 间的矩形的高;
间的矩形的高;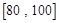 之间的学生中任选两人进行某项研究,求至少有一人分数在
之间的学生中任选两人进行某项研究,求至少有一人分数在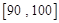 之间的概率.
之间的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
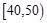 ,
,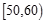 ,…,
,…, 后得到如下频率分布直方图.
后得到如下频率分布直方图.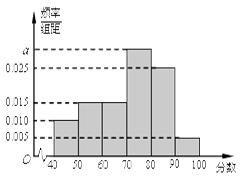
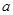 的值
的值查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
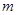 元的奖金;若中两次奖,则共获得数额为
元的奖金;若中两次奖,则共获得数额为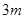 元的奖金;若中3次奖,则共获得数额为
元的奖金;若中3次奖,则共获得数额为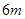 元的奖金。假设顾客每次抽奖中获的概率都是
元的奖金。假设顾客每次抽奖中获的概率都是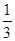 ,请问:商场将奖金数额m最高定为多少元,才能使促销方案对商场有利?
,请问:商场将奖金数额m最高定为多少元,才能使促销方案对商场有利?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com