
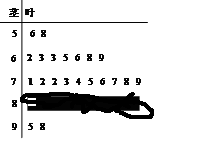

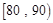 之间的频数,并计算频率分布直方图中
之间的频数,并计算频率分布直方图中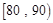 间的矩形的高;
间的矩形的高;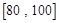 之间的学生中任选两人进行某项研究,求至少有一人分数在
之间的学生中任选两人进行某项研究,求至少有一人分数在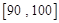 之间的概率.
之间的概率.科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 );
);查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
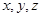 分别表示甲,乙,丙3个盒中的球数.
分别表示甲,乙,丙3个盒中的球数.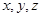 依次成公差大于0的等差数列的概率;
依次成公差大于0的等差数列的概率;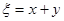 ,求随机变量
,求随机变量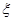 的概率分布列和数学期望.
的概率分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
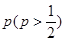 ,且各局胜负相互独立.已知
,且各局胜负相互独立.已知 .
.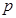 的值;
的值;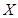 表示比赛停止时已比赛的局数,求随机变量
表示比赛停止时已比赛的局数,求随机变量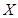 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
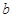 和
和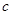 分别是先后抛掷一枚骰子得到的点数,用随机变量
分别是先后抛掷一枚骰子得到的点数,用随机变量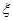 表示方程
表示方程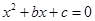 实根的个数(重根按一个计).
实根的个数(重根按一个计).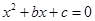 有实根的概率;
有实根的概率;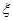 的分布列和数学期望;
的分布列和数学期望;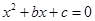 有实根的概率.
有实根的概率.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com