练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，已知平行六面体，点是上底面的中心，且， ，，则用，，表示向量为(   )

    A．   　　   B．

    C． 　 　  　　D．



    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    某地农业监测部门统计发现：该地区近几年的生猪收购价格每四个月会重复出现，但生猪养殖成本逐月递增．下表是今年前四个月的统计情况：

    月份

    1月份

    2月份

    3月份

    4月份

    收购价格（元/斤）

    6

    7

    6

    5

    养殖成本（元/斤）

    3

    4

    4．6

    5

    现打算从以下两个函数模型：①，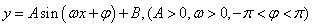

    ②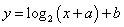中选择适当的函数模型，分别来拟合今年生猪收购价格（元/斤）与相应月份之间的函数关系、养殖成本（元/斤）与相应月份之间的函数关系．

    （1）请你选择适当的函数模型，分别求出这两个函数解析式；

    （2）按照你选定的函数模型，帮助该部门分析一下，今年该地区生猪养殖户在接下来的月份里有没有可能亏损?

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知递增的等比数列{an}满足a2＋a3＋a4＝28，且a3＋2是a2、a4的等差中项．

    (1)求数列{an}的通项公式；

    (2)若bn＝log2an＋1，Sn是数列{bn}的前n项和，求使Sn>42＋4n成立的n的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     椭圆 的焦点为，点P在椭圆上，若，则的大小为  _______

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    下列命题中的假命题是（   ）

    A.              B.

    C.                D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知向量，，若成1200的角，则k=        ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    　　在四棱锥中，底面，，, 且.

    (1)若是的中点，求证：平面;

    (2)求二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数是奇函数，且.

    （Ⅰ）求函数的解析式；

    （Ⅱ）用定义证明函数在上的单调性．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    根据气象预报, 某地区近期有小洪水的概率为0.25, 有大洪水的概率为0.01.该地区某工地上有一台大型设备, 遇到大洪水时要损失60000元, 遇到小洪水时要损失10000元. 为保护设备, 有以下3种方案：

        方案1：运走设备, 搬运费为3800元.

        方案2：建保护围墙, 建设费为2000元, 但围墙只能防小洪水.

        方案3：不采取措施.

        试比较哪一种方案好.

    查看答案和解析>>

    同步练习册答案