
【题目】2006 年 8 月中旬 , 湖南省资兴市遇到了百年不遇的洪水灾害 . 在资兴市的东江湖岸边的点 O 处(可视湖岸为直线) 停放着一只救人的小船,由于缆绳突然断开,小船被风刮跑,其方向与湖岸成 15°,, 速度为2.5 km/ h ,同时,岸上有一人从同一地点开始追赶小船 .已知他在岸上追的速度为4 km/ h ,在水中游的速度为 2 km/h .问此人能否追上小船? 若小船速度改变 ,则小船能被此人追上的最大速度是多少 ?
科目:高中数学 来源: 题型:
【题目】某校有教师400人,对他们进行年龄状况和学历的调查,其结果如下:
学历 | 35岁以下 | 35-55岁 | 55岁及以上 |
本科 |
| 60 | 40 |
硕士 | 80 | 40 |
|
(1)若随机抽取一人,年龄是35岁以下的概率为![]() ,求
,求![]() ;
;
(2)在35-55岁年龄段的教师中,按学历状况用分层抽样的方法,抽取一个样本容量为5的样本,然后在这5名教师中任选2人,求两人中至多有1人的学历为本科的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】孝感市旅游局为了了解双峰山景点在大众中的熟知度,从年龄在15~65岁的人群中随机抽取n人进行问卷调查,把这n人按年龄分成5组:第一组[15,25),第二组[25,35),第三组[35,45),第四组[45,55),第五组[55,65],得到的样本的频率分布直方图如右:

调查问题是“双峰山国家森林公园是几A级旅游景点?”每组中回答正确的人数及回答正确的人数占本组的频率的统计结果如下表.
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 |
第1组 | [15,25) | 5 | 0.5 |
第2组 | [25,35) | 18 | x |
第3组 | [35,45) | y | 0.9 |
第4组 | [45,55) | 9 | a |
第5组 | [55,65] | 7 | b |
(1)分别求出n,x,y的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,求第2,3,4组每组各抽取多少人;
(3)在(2)抽取的6人中随机抽取2人,求所抽取的两人来自不同年龄组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
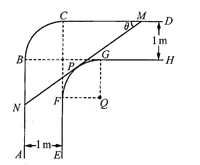
【题目】一走廊拐角处的横截面如图所示,已知内壁![]() 和外壁
和外壁![]() 都是半径为1m的四分之一圆弧,
都是半径为1m的四分之一圆弧,![]() 分别与圆弧
分别与圆弧![]() 相切于
相切于![]() 两点,
两点,![]() 且两组平行墙壁间的走廊宽度都是1m.
且两组平行墙壁间的走廊宽度都是1m.
(1)若水平放置的木棒![]() 的两个端点
的两个端点![]() 分别在外壁
分别在外壁![]() 和
和![]() 上,且木棒与内壁圆弧相切于点
上,且木棒与内壁圆弧相切于点![]() 设
设![]() 试用
试用![]() 表示木棒
表示木棒![]() 的长度
的长度![]()
(2)若一根水平放置的木棒能通过该走廊拐角处,求木棒长度的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为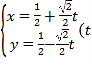 为参数), 椭圆C的参数方程为
为参数), 椭圆C的参数方程为![]() 为参数)。在平面直角坐标系中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点A的极坐标为(2,
为参数)。在平面直角坐标系中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点A的极坐标为(2, ![]()
(1)求椭圆C的直角坐标方程和点A在直角坐标系下的坐标
(2)直线l与椭圆C交于P,Q两点,求△APQ的面积
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l过点A(-1,0)且与⊙B:![]() 相切于点D,以坐标轴为对称轴的双曲线E过点D,一条渐近线平行于l,则E的离心率为( )
相切于点D,以坐标轴为对称轴的双曲线E过点D,一条渐近线平行于l,则E的离心率为( )
A. ![]() B. 2 C.
B. 2 C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com