
【题目】若四位数![]() 的各位数码
的各位数码![]() 中,任三个数码皆可构成一个三角形的三条边长,则称n为“四位三角形数”.试求所有四位三角形数的个数.
中,任三个数码皆可构成一个三角形的三条边长,则称n为“四位三角形数”.试求所有四位三角形数的个数.
【答案】1681
【解析】
称(![]() )为n的数码组,则
)为n的数码组,则![]()
![]()
1.当数码组只含一个值,即![]()
![]() 时,共得9个n值.
时,共得9个n值.
2.当数码组恰含两个值![]()
i.数码组为![]() 型,则任取三个数码皆可构成三角形
型,则任取三个数码皆可构成三角形
对于每个![]() ,b可取
,b可取![]() 个值
个值
则数码组个数为![]() .
.
对于每组![]() ,b有4种占位方式.
,b有4种占位方式.
于是,这种n有![]() 个.
个.
ii.数码组为![]() 型,据构成三角形条件,有
型,据构成三角形条件,有![]() .
.
如下表,共得16个数码组,对于每组![]() ,
,![]() 有4种占位方式.
有4种占位方式.
于是,这种n有![]() 个.
个.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 1 | 2 | 3 | 4 | 3 | 2 | 1 | 0 |
iii.数码组为![]() 型,据构成三角形条件,有
型,据构成三角形条件,有![]() .
.
同上得16个数码组,对于每组![]() ,两个
,两个![]() 有
有![]() 种占位方式.
种占位方式.
则这种n有![]() 个.
个.
以上共计144+64+96=304个.
3.当数码组恰含三个值![]() .
.
i.数码组为![]() 型,据构成三角形条件,则有
型,据构成三角形条件,则有![]() .
.
这种![]() 有14组,每组中
有14组,每组中![]() 有
有![]() 种占位方式.
种占位方式.
于是,这种n有![]() 个.
个.
ii.数码组为![]() 型,
型,![]() .
.
此条件等价于![]() 中取3个不同的数构成三角形的方法数.
中取3个不同的数构成三角形的方法数.
有34组,每组中![]() 有
有![]() 种占位方式.
种占位方式.
于是,这种n有![]() 个.
个.
iii.数码组为![]() 型,
型,![]() ,同情况ii,有
,同情况ii,有![]() 个n值.
个n值.
以上共计168+408+408=984个.
4. ![]() 互不相同,则有
互不相同,则有![]() .
.
这种![]() 有16组,每组有
有16组,每组有![]() 种排法.
种排法.
共得![]() 个n值.
个n值.
综上,全部四位三角形数n的个数为9+304+984+384=1681(个)


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
【题目】已知点P是椭圆![]() 上的动点,
上的动点,![]() 、
、![]() 为椭圆的左、右焦点,O为坐标原点,若M是
为椭圆的左、右焦点,O为坐标原点,若M是![]() 的角平分线上的一点,且F1M⊥MP,则|OM|的取值范围是( )
的角平分线上的一点,且F1M⊥MP,则|OM|的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2006 年 8 月中旬 , 湖南省资兴市遇到了百年不遇的洪水灾害 . 在资兴市的东江湖岸边的点 O 处(可视湖岸为直线) 停放着一只救人的小船,由于缆绳突然断开,小船被风刮跑,其方向与湖岸成 15°,, 速度为2.5 km/ h ,同时,岸上有一人从同一地点开始追赶小船 .已知他在岸上追的速度为4 km/ h ,在水中游的速度为 2 km/h .问此人能否追上小船? 若小船速度改变 ,则小船能被此人追上的最大速度是多少 ?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了检验两种不同的课堂教学模式对学生的成绩是否有影响,现从高二年级的甲(实行的“问题——探究式”)、乙(实行的“自学——指导式”)两个班中每班任意抽取20名学生进行测试,他们的成绩(总分150分)分布茎叶图如图所示(以十位百位为茎,个位为叶):

(1)若从参与测试的学生试卷中挑选2份卷面分数为90~100分的试着进行卷面分析,求抽取的2份试卷恰好每班1份的概率?
(2)记成绩在120分以上(包括120分)为优秀,其他的成绩为一般,请完成下面![]() 列联表,并分析是否有足够的把握(90%以上)认为这两种课堂教学模式对学生的成绩有影响?
列联表,并分析是否有足够的把握(90%以上)认为这两种课堂教学模式对学生的成绩有影响?
成绩 班级 | 优秀人数 | 一般人数 | 总计 |
甲班 | |||
乙班 | |||
总计 |
附: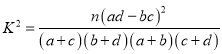
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】a,b为空间中两条互相垂直的直线,等腰直角三角形ABC的直角边AC所在直线与a,b都垂直,斜边AB以直线AC为旋转轴旋转,有下列结论:
①当直线AB与a成60°角时,AB与b成30°角;
②当直线AB与a成60°角时,AB与b成60°角;
③直线AB与a所成角的最小值为45°;
④直线AB与a所成角的最大值为60°.
其中正确的是________.(填写所有正确结论的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】里氏震级M的计算公式为:M=lgA﹣lgA0,其中A是测震仪记录的地震曲线的最大振幅,是相应的标准地震的振幅,假设在一次地震中,测震仪记录的最大振幅是1000,此时标准地震的振幅A0为0.001,则此次地震的震级为 级;9级地震的最大的振幅是5级地震最大振幅的 倍.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正多面体共有5种,即正四面体、正六面体、正八面体、正十二面体和正二十面体.任一个正多面体都有内切球和外接球,若一个半径为1的球既是一个正四面体的内切球,又是一个正六面体的外接球,则这两个多面体的顶点之间的最短距离为( )
A.![]() -1B.1C.2
-1B.1C.2![]() -1D.2
-1D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC的面积为![]()
(1)求sinBsinC;
(2)若6cosBcosC=1,a=3,求△ABC的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com