【题目】已知正多面体共有5种，即正四面体、正六面体、正八面体、正十二面体和正二十面体.任一个正多面体都有内切球和外接球，若一个半径为1的球既是一个正四面体的内切球，又是一个正六面体的外接球，则这两个多面体的顶点之间的最短距离为（ ）
A.
－1B.1C.2
－1D.2
全能闯关100分系列答案科目：高中数学 来源： 题型：
【题目】已知直线l的参数方程为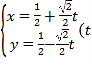
为参数）， 椭圆C的参数方程为
为参数）。在平面直角坐标系中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点A的极坐标为(2, 
(1)求椭圆C的直角坐标方程和点A在直角坐标系下的坐标
(2)直线l与椭圆C交于P,Q两点,求△APQ的面积
查看答案和解析>>
科目：高中数学 来源： 题型：
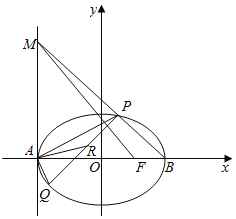
【题目】已知椭圆C：
的左右顶点为A、B，右焦点为F，一条准线方程是
，短轴一端点与两焦点构成等边三角形，点P、Q为椭圆C上异于A、B的两点，点R为PQ的中点
求椭圆C的标准方程；
直线PB交直线
于点M，记直线PA的斜率为
，直线FM的斜率为
，求证：
为定值；
若
，求直线AR的斜率的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某校高三文科
名学生参加了
月份的高考模拟考试，学校为了了解高三文科学生的历史、地理学习情况，从名学生中抽取
名学生的成绩进行统计分析，抽出的名学生的地理、历史成绩如下表：
地理 历史 | [80,100] | [60,80） | [40,60） |
[80,100] | 8 | m | 9 |
[60,80） | 9 | n | 9 |
[40,60） | 8 | 15 | 7 |
若历史成绩在[80,100]区间的占30%，
（1）求
的值；
（2）请根据上面抽出的名学生地理、历史成绩，填写下面地理、历史成绩的频数分布表：
[80,100] | [60,80） | [40,60） | |
地理 | |||
历史 |
根据频数分布表中的数据估计历史和地理的平均成绩及方差（同一组数据用该组区间的中点值作代表），并估计哪个学科成绩更稳定.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知直线l过点A(-1,0)且与⊙B：
相切于点D，以坐标轴为对称轴的双曲线E过点D，一条渐近线平行于l，则E的离心率为（ ）
A. 
B. 2 C. 
D. 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，直三棱柱ABC-A1B1C1中，D,E分别是AB，BB1的中点.
（Ⅰ）证明： BC1//平面A1CD;
（Ⅱ）设AA1= AC=CB=2，AB=2
，求三棱锥C一A1DE的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
