
【题目】某校有教师400人,对他们进行年龄状况和学历的调查,其结果如下:
学历 | 35岁以下 | 35-55岁 | 55岁及以上 |
本科 |
| 60 | 40 |
硕士 | 80 | 40 |
|
(1)若随机抽取一人,年龄是35岁以下的概率为![]() ,求
,求![]() ;
;
(2)在35-55岁年龄段的教师中,按学历状况用分层抽样的方法,抽取一个样本容量为5的样本,然后在这5名教师中任选2人,求两人中至多有1人的学历为本科的概率.
科目:高中数学 来源: 题型:
【题目】如图所示,在正方体![]() 中,点
中,点![]() 是棱
是棱![]() 上的一个动点,平面
上的一个动点,平面![]() 交棱
交棱![]() 于点
于点![]() .给出下列命题:
.给出下列命题:
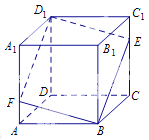
①存在点![]() ,使得
,使得![]() //平面
//平面![]() ;
;
②对于任意的点![]() ,平面
,平面![]() 平面
平面![]() ;
;
③存在点![]() ,使得
,使得![]() 平面
平面![]() ;
;
④对于任意的点![]() ,四棱锥
,四棱锥![]() 的体积均不变.
的体积均不变.
其中正确命题的序号是______.(写出所有正确命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知ω>0,0<φ<π,直线![]() 和
和![]() 是函数f(x)=sin(ωx+φ)图象的两条相邻的对称轴,若将函数f(x)图象上每一点的横坐标变为原来的
是函数f(x)=sin(ωx+φ)图象的两条相邻的对称轴,若将函数f(x)图象上每一点的横坐标变为原来的![]() 倍,纵坐标变为原来的2倍,则得到的图象的函数解析式是( )
倍,纵坐标变为原来的2倍,则得到的图象的函数解析式是( )
A.![]() B.
B.![]()
C.y=2cos2xD.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解本市的交通状况,某校高一年级的同学分成了甲、乙、丙三个组,从下午13点到18点,分别对三个路口的机动车通行情况进行了实际调查,并绘制了频率分布直方图(如图),记甲、乙、丙三个组所调查数据的标准差分别为![]() ,则它们的大小关系为( )
,则它们的大小关系为( )

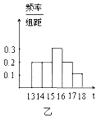
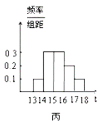
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2006 年 8 月中旬 , 湖南省资兴市遇到了百年不遇的洪水灾害 . 在资兴市的东江湖岸边的点 O 处(可视湖岸为直线) 停放着一只救人的小船,由于缆绳突然断开,小船被风刮跑,其方向与湖岸成 15°,, 速度为2.5 km/ h ,同时,岸上有一人从同一地点开始追赶小船 .已知他在岸上追的速度为4 km/ h ,在水中游的速度为 2 km/h .问此人能否追上小船? 若小船速度改变 ,则小船能被此人追上的最大速度是多少 ?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】a,b为空间中两条互相垂直的直线,等腰直角三角形ABC的直角边AC所在直线与a,b都垂直,斜边AB以直线AC为旋转轴旋转,有下列结论:
①当直线AB与a成60°角时,AB与b成30°角;
②当直线AB与a成60°角时,AB与b成60°角;
③直线AB与a所成角的最小值为45°;
④直线AB与a所成角的最大值为60°.
其中正确的是________.(填写所有正确结论的编号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com