练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数.

    （1）若，求函数f(x)的单调递增区间；

    （2）若，求函数在区间上的值域.

    【答案】（1）；（2）当时，值域为；当时，值域为；当时，值域为.

    【解析】

    （1）根据自变量范围化简函数，画出函数图像，根据图像得到单调区间.

    （2）根据自变量范围化简函数，讨论，，三种情况，根据单调性计算最值，再讨论和的大小关系得到答案.

    （1），画出函数图像，如图所示：

    根据图像知函数的单调增区间为和.

    （2），

    画出函数简图，如图所示：当时，二次函数对称轴为，

    当，即时，函数在上单调递增，

    故，

    ，故值域为；

    当，即时，，

    ，值域为；

    当时，，，

    ，取，即，

    解得或（舍去），

    故当时，，值域为；

    当时，，值域为.

    综上所述：当时，值域为；当时，值域为；当时，值域为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】有一段“三段论”，其推理是这样的：对于可导函数，若，则是函数的极值点,因为函数满足，所以是函数的极值点”，结论以上推理　　

    A. 大前提错误B. 小前提错误C. 推理形式错误D. 没有错误

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中．

    (1)试讨论函数的单调性；

    (2)若，且函数有两个零点，求实数的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知二次函数f（x）=x2+bx+c，若对任意的x1，x2∈[-1，1]，有|f（x1）-f（x2）|≤6，则b的取值范围是（　　）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（1）由0，1，2，…，9这十个数字组成的无重复数字的四位数中，十位数字与千位数字之差的绝对值等于7的四位数的个数共有几种？

    （2）我校高三学习雷锋志愿小组共有16人，其中一班、二班、三班、四班各4人，现在从中任选3人，要求这三人不能是同一个班级的学生，且在三班至多选1人，求不同的选取法的种数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】[选修4-4：坐标系与参数方程]:在直角坐标系中，曲线的参数方程为（为参数），以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为.

    （1）求曲线，的直角坐标方程；

    （2）判断曲线，是否相交，若相交，请求出交点间的距离；若不相交，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直三棱柱中，，，，，为的中点.

    （1）证明：平面；

    （2）求直线与平面所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校有教师400人，对他们进行年龄状况和学历的调查，其结果如下：

    学历

    35岁以下

    35-55岁

    55岁及以上

    本科

    60

    40

    硕士

    80

    40

    (1)若随机抽取一人，年龄是35岁以下的概率为，求；

    (2)在35-55岁年龄段的教师中，按学历状况用分层抽样的方法，抽取一个样本容量为5的样本，然后在这5名教师中任选2人，求两人中至多有1人的学历为本科的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线l的参数方程为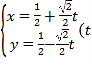为参数）， 椭圆C的参数方程为为参数）。在平面直角坐标系中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点A的极坐标为(2,

    (1)求椭圆C的直角坐标方程和点A在直角坐标系下的坐标

    (2)直线l与椭圆C交于P,Q两点,求△APQ的面积

    查看答案和解析>>

    同步练习册答案