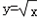练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    给定函数①，②y=log2（x+1），③y=|x﹣1|，④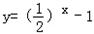，其中在区间（0，1）上单调递减的函数序号是 
     [     ]
    A．①②
    B．②③
    C．③④
    D．①④
    C
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知二次函数f（x）=ax2+8x+3．
    （1）若函数f（x）=ax2+8x+3的图象恒在直线y=5的下方，求实数a的范围；
    （2）对于给定的负数a，有一个最大的正数l（a），使得在整个区间[0，l（a）]上，不等式|f（x）|≤5都成立．问a为何值时l（a）最大？求出这个最大的l（a），证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2011•江西模拟）已知函数f（x）=ax-lnx+1（a∈R），g（x）=xe1-x．
    （1）求函数g（x）在区间（0，e]上的值域；
    （2）是否存在实数a，对任意给定的x0∈（0，e]，在区间[1，e]上都存在两个不同的xi（i=1，2），使得f（xi）=g（x0）成立．若存在，求出a的取值范围；若不存在，请说明理由．
    （3）给出如下定义：对于函数y=F（x）图象上任意不同的两点A（x1，y1），B（x2，y2），如果对于函数y=F（x）图象上的点M（x0，y0）（其中x0=
    x1+x22
    )    总能使得F（x1）-F（x2）=F'（x0）（x1-x2）成立，则称函数具备性质“L”，试判断函数f（x）是不是具备性质“L”，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

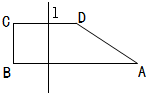    如图所示直角梯形ABCD中上底CD=2，下底AB=4，高BC=1直线l与线段AB垂直相交，设A点到直线l的距离为x，直线l截梯形ABCD所得的位于l左方的图形面积为y．
    （1）求函数y=f（x）解析式；
    （2）在给定的坐标系内画出y=f（x）的图象．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知点集，其中，，点列在L中，为L与y轴的交点，等差数列的公差为1，。

    （1）求数列的通项公式；

    （2）若＝，令；试用解析式写出关于的函数。

    （3）若＝，给定常数m(),是否存在，使得 ，若存在，求出的值；若不存在，请说明理由。

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年江西省重点中学协作体高三第三次联考数学试卷（理科）（解析版） 题型：解答题

    已知函数f（x）=ax-lnx+1（a∈R），g（x）=xe1-x．
    （1）求函数g（x）在区间（0，e]上的值域；
    （2）是否存在实数a，对任意给定的x∈（0，e]，在区间[1，e]上都存在两个不同的xi（i=1，2），使得f（xi）=g（x）成立．若存在，求出a的取值范围；若不存在，请说明理由．
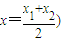    （3）给出如下定义：对于函数y=F（x）图象上任意不同的两点A（x1，y1），B（x2，y2），如果对于函数y=F（x）图象上的点M（x，y）（其中总能使得F（x1）-F（x2）=F'（x）（x1-x2）成立，则称函数具备性质“L”，试判断函数f（x）是不是具备性质“L”，并说明理由．

    查看答案和解析>>

    同步练习册答案