【题目】函数f（x）= 
+ 
的定义域为（用集合或区间表示）．
【答案】[﹣1，1）∪（1，2）∪（2，+∞）
【解析】解：由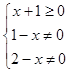 
，解得﹣1≤x＜1或1＜x＜2或x＞2．∴函数f（x）= 
+ 
的定义域为[﹣1，1）∪（1，2）∪（2，+∞）．
所以答案是：[﹣1，1）∪（1，2）∪（2，+∞）．
【考点精析】解答此题的关键在于理解函数的定义域及其求法的相关知识，掌握求函数的定义域时，一般遵循以下原则：①
是整式时，定义域是全体实数;②是分式函数时，定义域是使分母不为零的一切实数;③是偶次根式时，定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零，当对数或指数函数的底数中含变量时，底数须大于零且不等于1,零（负）指数幂的底数不能为零．
科目：高中数学 来源： 题型：
【题目】（本小题满分12分）某企业生产的一批产品中有一、二、三等品及次品共四个等级，1件不同等级产品的利润（单位：元）如表1，从这批产品中随机抽取出1件产品，该件产品为不同等级的概率如表2.
等级 | 一等品 | 二等品 | 三等品 | 次品 |
|
| |
|
|
等级 | 一等品 | 二等品 | 三等品 | 次品 |
利润 | |
|
|
|
表1 表2
若从这批产品中随机抽取出的1件产品的平均利润(即数学期望)为
元.
(1) 设随机抽取1件产品的利润为随机变量
，写出
的分布列并求出
的值；
(2) 从这批产品中随机取出3件产品，求这3件产品的总利润不低于17元的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
，
．
（1）若
，求函数
的图象在
处的切线方程；
（2）若
，试讨论方程
的实数解的个数；
（3）当
时，若对于任意的
，都存在
，使得
，求满足条件的正整数
的取值的集合．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】三棱锥S﹣ABC中，∠SBA=∠SCA=90°，△ABC是斜边AB=a的等腰直角三角形，则以下结论中： ①异面直线SB与AC所成的角为90°；
②直线SB⊥平面ABC；
③面SBC⊥面SAC；
④点C到平面SAB的距离是 
．
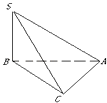
其中正确结论的序号是 ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为贯彻落实教育部6部门《关于加快发展青少年校园足球的实施意见》，全面提高我市中学生的体质健康水平，培养拼搏意识和团队精神，普及足球知识和技能，市教体局决定举行春季校园足球联赛．为迎接此次联赛，甲中学选拔了20名学生组成集训队，现统计了这20名学生的身高，记录入如表：（设ξ为随机变量） 
身高（cm） | 168 | 174 | 175 | 176 | 178 | 182 | 185 | 188 |
人数 | 1 | 2 | 4 | 3 | 5 | 1 | 3 | 1 |
（1）请计算这20名学生的身高的中位数、众数，并补充完成下面的茎叶图；
（2）身高为185cm和188cm的四名学生分别记为A，B，C，D，现从这四名学生选2名担任正副门将，请利用列举法列出所有可能情况，并求学生A入选门将的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了调查观众对某电视剧的喜爱程度，某电视台在甲乙两地随机抽取了8名观众做问卷调查，得分结果如图所示：
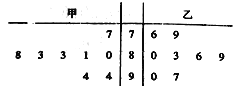
（1）计算甲地被抽取的观众问卷得分的中位数和乙地被抽取的观众问卷得分的平均数；
（2）用频率估计概率，若从乙地的所有观众中再随机抽取4人进行问卷调查，记问卷分数不低于80分的人数为
，求
的分布列与期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】过直线x=﹣2上的动点P作抛物线y2=4x的两条切线PA，PB，其中A，B为切点．
（1）若切线PA，PB的斜率分别为k1 ， k2 ， 求证：k1k2为定值；
（2）求证：直线AB恒过定点．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图示：半圆O的直径为2，A为直径延长线上的一点，OA=2，B为半圆上任意一
点，以AB为一边作等边三角形ABC．则四边形OACB的面积最大值是 ． 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
