
分析 (Ⅰ)通过a1=1,${a_{n+1}}=\frac{{{a_n}+4}}{{{a_n}+1}}$计算求出a2,a3的值;一方面,利用${a_{n+1}}-2=\frac{{{a_n}+4}}{{{a_n}+1}}-2=-\frac{{{a_n}-2}}{{{a_n}+1}}$整理可知a2n+1-2与a2n-1-2同号,进而可知a2n+1<2;另一方面,通过作差计算可知a2n+1>a2n-1,从而可得结论;
(Ⅱ)利用${a_{n+1}}=\frac{{{a_n}+4}}{{{a_n}+1}}$计算可知$\frac{{{b_{n+1}}}}{b_n}=\frac{1}{{2{a_{2n-1}}+5}}$,结合1≤a2n-1<a2n+1<2可知$\frac{1}{9}<\frac{{{b_{n+1}}}}{b_n}≤\frac{1}{7}$,利用累乘法可知$\frac{1}{{9}^{n-1}}$≤bn<$\frac{1}{{7}^{n-1}}$,进而利用等比数列的求和公式计算即得结论.
解答 (Ⅰ)解:∵a1=1,${a_{n+1}}=\frac{{{a_n}+4}}{{{a_n}+1}}$,
∴${a_2}=\frac{5}{2}$,a3=$\frac{13}{7}$;
下证:a2n-1<a2n+1<2.
一方面,${a_{n+1}}-2=\frac{{{a_n}+4}}{{{a_n}+1}}-2=-\frac{{{a_n}-2}}{{{a_n}+1}}$,
所以$\frac{{{a_{n+1}}-2}}{{{a_n}-2}}=-\frac{1}{{{a_n}+1}}$,
由题可知an>0,所以$\frac{{{a_{n+1}}-2}}{{{a_n}-2}}<0$,即an+1-2与an-2异号,
故an+2-2与an-2同号,于是a2n+1-2与a2n-1-2同号,
又∵a1-2=-1<0,∴a2n+1<2;
另一方面,${a_{2n+1}}-{a_{2n-1}}=\frac{{{a_{2n}}+4}}{{{a_{2n}}+1}}-{a_{2n-1}}=\frac{{\frac{{{a_{2n-1}}+4}}{{{a_{2n-1}}+1}}+4}}{{\frac{{{a_{2n-1}}+4}}{{{a_{2n-1}}+1}}+1}}-{a_{2n-1}}=\frac{{5{a_{2n-1}}+8}}{{2{a_{2n-1}}+5}}-{a_{2n-1}}=\frac{{-2({{a_{2n-1}}^2-4})}}{{2{a_{2n-1}}+5}}$,
由a2n-1<2知a2n+1-a2n-1>0,即a2n+1>a2n-1,
综上所述:a2n-1<a2n+1<2;
(Ⅱ)证明:${a_{2n+1}}-2=-\frac{{{a_{2n}}-2}}{{{a_{2n}}+1}}=-\frac{{\frac{{{a_{2n-1}}+4}}{{{a_{2n-1}}+1}}-2}}{{\frac{{{a_{2n-1}}+4}}{{{a_{2n-1}}+1}}+1}}=\frac{{{a_{2n-1}}-2}}{{2{a_{2n-1}}+5}}$,
由bn=|a2n-1-2|知$\frac{{{b_{n+1}}}}{b_n}=\frac{1}{{2{a_{2n-1}}+5}}$,
又1≤a2n-1<a2n+1<2,所以$\frac{1}{9}<\frac{{{b_{n+1}}}}{b_n}≤\frac{1}{7}$,
而b1=1,所以当n≥2时${b_n}={b_1}•\frac{b_2}{b_1}•…•\frac{b_n}{{{b_{n-1}}}}≤{({\frac{1}{7}})^{n-1}}$,
同理可知:${b_n}>{({\frac{1}{9}})^{n-1}}$,
故Sn=b1+b2+…+bn$≤1+\frac{1}{7}+{({\frac{1}{7}})^2}+…+{({\frac{1}{7}})^{n-1}}=\frac{{1-{{({\frac{1}{7}})}^n}}}{{1-\frac{1}{7}}}<\frac{7}{6}$,
${S_n}={b_1}+{b_2}+…+{b_n}>\frac{{1-{{({\frac{1}{9}})}^n}}}{{1-\frac{1}{9}}}=\frac{9}{8}[{1-{{({\frac{1}{9}})}^n}}]$,
综上:$\frac{9}{8}[{1-{{({\frac{1}{9}})}^n}}]<{S_n}<\frac{7}{6}$.
点评 本题是一道关于数列与不等式的综合题,考查运算求解能力,涉及放缩法,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | -7 | B. | -$\frac{1}{7}$ | C. | 7 | D. | $\frac{1}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若α⊥β,a⊥b,且b与l不垂直,则a⊥l | B. | 若α⊥β,b⊥l,则a⊥b | ||
| C. | 若a⊥b,b⊥l,且a与l不平行,则α⊥β | D. | 若a⊥l,b⊥l,则α⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
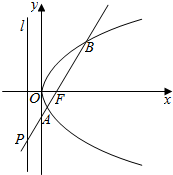 已知抛物线C:y2=2px(p>0)焦点为F(1,0),过F作斜率为k的直线交抛物线C于A、B两点,交其准线l于P点.
已知抛物线C:y2=2px(p>0)焦点为F(1,0),过F作斜率为k的直线交抛物线C于A、B两点,交其准线l于P点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈Z,都有x2+2x+m≤0 | B. | ?x∈Z,使x2+2x+m>0 | ||
| C. | ?x∈Z,都有x2+2x+m>0 | D. | 不存在x∈Z,使x2+2x+m>0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com