
【题目】已知圆C过点M(0,﹣2),N(3,1),且圆心C在直线x+2y+1=0上.
(1)求圆C的方程;
(2)问是否存在满足以下两个条件的直线l:①斜率为1;②直线被圆C截得的弦为AB,以AB为直径的圆C1过原点.若存在这样的直线,请求出其方程;若不存在,说明理由.
【答案】
(1)解:设圆C的方程为x2+y2+Dx+Ey+F=0
则 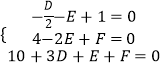 解得D=﹣6,E=4,F=4
解得D=﹣6,E=4,F=4
∴圆C方程为x2+y2﹣6x+4y+4=0
(2)解:设直线存在,其方程为y=x+b,它与圆C的交点设为A(x1,y1)、B(x2,y2),
则由 ![]() 得2x2+2(b﹣1)x+b2+4b+4=0(*)
得2x2+2(b﹣1)x+b2+4b+4=0(*)
∴ 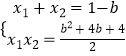
∴y1y2=(x1+b)(x2+b)= ![]() ,
,
∵AB为直径,∴,∠AOB=90°,∴OA2+OB2=AB2,
∴ ![]()
得x1x2+y1y2=0,
∴ ![]() ,
,
即b2+4b+4+b(1﹣b)+b2=0,b2+5b+4=0,∴b=﹣1或b=﹣4
容易验证b=﹣1或b=﹣4时方程(*)有实根.
故存在这样的直线l有两条,其方程是y=x﹣1或y=x﹣4.
【解析】(1)设圆C的方程为x2+y2+Dx+Ey+F=0,利用点在圆上,圆心在直线上,列出方程组,解得D,E,F,即可求得圆C方程.(2)设直线存在,其方程为y=x+b,它与圆C的交点设为A(x1 , y1)、B(x2 , y2),利用直线与圆的方程联立方程组,利用韦达定理,推出x1x2 , y1y2 , 利用垂直关系得到 ![]() ,求得b=﹣1或b=﹣4时方程(*)有实根.说明存在这样的直线l有两条,即可.
,求得b=﹣1或b=﹣4时方程(*)有实根.说明存在这样的直线l有两条,即可.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的右焦点为
的右焦点为![]() ,右顶点为
,右顶点为![]() .已知
.已知![]() ,其中
,其中![]() 为原点,
为原点, ![]() 为椭圆的离心率.
为椭圆的离心率.
(1)求椭圆的方程及离心率![]() 的值;
的值;
(2)设过点![]() 的直线
的直线![]() 与椭圆交于点
与椭圆交于点![]() (
(![]() 不在
不在![]() 轴上),垂直于
轴上),垂直于![]() 的直线与
的直线与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .若
.若![]() ,且
,且![]() ,求直线
,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1C1C. 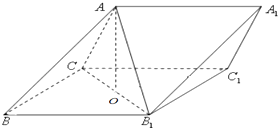
(1)证明:B1C⊥AB;
(2)若AC⊥AB1 , ∠CBB1=60°,BC=2,求B1到平面ABC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将参加数学竞赛的1000名学生编号如下:0001,0002,003,…,1000,打算从中抽取一个容量为50的样本,按系统抽样的方法把编号分成50个部分,如果第一部分编号为0001,0002,0003,…,0020,第一部分随机抽取一个号码为0013,那么抽取的第40个号码 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆心为C的圆经过点A(0,2)和B(1,1),且圆心C在直线l:x+y+5=0上.
(1)求圆C的标准方程;
(2)若P(x,y)是圆C上的动点,求3x﹣4y的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数y=2sin(2x+ ![]() )的图象,只需把函数y=2sinx的图象( )
)的图象,只需把函数y=2sinx的图象( )
A.向左平移 ![]() 个单位长度,再把所得各点的横坐标变为原来的2倍(纵坐标不变)
个单位长度,再把所得各点的横坐标变为原来的2倍(纵坐标不变)
B.向左平移 ![]() 个单位长度,再把所得各点的横坐标变为原来的
个单位长度,再把所得各点的横坐标变为原来的 ![]() 倍(纵坐标不变)
倍(纵坐标不变)
C.各点的纵坐标不变、横坐标变为原来的2倍,再把所得图象向左平移 ![]() 个单位长度
个单位长度
D.各点的纵坐标不变、横坐标变为原来的 ![]() 倍,再把所得图象向左平移
倍,再把所得图象向左平移 ![]() 个单位长度
个单位长度
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com