
 )三点.
)三点.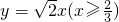 上(非端点)任意一点,由点P向椭圆C引两条切线PQ、PT(Q、T为切点),求证:直线QT的斜率为常数.
上(非端点)任意一点,由点P向椭圆C引两条切线PQ、PT(Q、T为切点),求证:直线QT的斜率为常数. )三点坐标代入解得
)三点坐标代入解得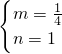 ,
, +y2=1.
+y2=1.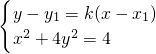 化简为关于(x-x1)的一元二次方程,
化简为关于(x-x1)的一元二次方程,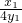
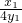 (x-x1).即直线的方程为x1x+4y1y-4=0.
(x-x1).即直线的方程为x1x+4y1y-4=0. t)(t>
t)(t> )在直线PQ上,所以tx1+4
)在直线PQ上,所以tx1+4 ty1-4=0
ty1-4=0 ty-4=0上.同理,点T(x2,y2)也在直线tx+4
ty-4=0上.同理,点T(x2,y2)也在直线tx+4 ty-4=0上,
ty-4=0上, ty-4=0,
ty-4=0,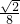 (常数).
(常数).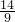 ,
, ),Q(2,0)所以kQT=-
),Q(2,0)所以kQT=-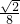 (常数)
(常数)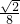 .
. )三点的坐标代入,即可求出椭圆C的方程;
)三点的坐标代入,即可求出椭圆C的方程;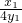 进而求出切线方程,再利用P(t,
进而求出切线方程,再利用P(t, t)(t>
t)(t> )在直线PQ上,找到点Q(x1,y1)所在直线方程,同样的方法,找到点T(x2,y2)也在直线tx+4
)在直线PQ上,找到点Q(x1,y1)所在直线方程,同样的方法,找到点T(x2,y2)也在直线tx+4 ty-4=0上,就可求出直线QT的斜率为常数的值.
ty-4=0上,就可求出直线QT的斜率为常数的值.

科目:高中数学 来源: 题型:解答题
 )的距离比它到x轴的距离大
)的距离比它到x轴的距离大 ,设动点M的轨迹是曲线E.
,设动点M的轨迹是曲线E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 =(sinx,1),
=(sinx,1), =(
=( Acosx,
Acosx, cos2x)(A>0),函数f(x)=
cos2x)(A>0),函数f(x)= •
• 的最大值为6.
的最大值为6. 个单位,再将所得图象各点的横坐标缩短为原来的
个单位,再将所得图象各点的横坐标缩短为原来的 倍,纵坐标不变,得到函数y=g(x)的图象.求g(x)在[0,
倍,纵坐标不变,得到函数y=g(x)的图象.求g(x)在[0,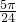 ]上的值域.
]上的值域.查看答案和解析>>
科目:高中数学 来源: 题型:单选题
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com