练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设a为实数，函数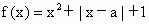，xÎ R，

    (1)讨论f(x)的奇偶性；

    (2)求f(x)的最小值．

    答案：略
    解析：

    从函数的奇偶性和最小值入手，正确地运用分类讨论．

    解：(1)当a=0时，此时，函数f(x)是偶函数．

    当a¹ 0时，，，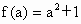

    所以f(－a)¹ f(a)，f(－a)¹ －f(a)．

    此时，函数f(x)既不是奇函数也不是偶函数．

    (2)当x≤a时，，

    若，则函数f(x)在(－¥ ,a]上单调递减，从而函数f(x)在(－¥ ，a]上的最小值为．

    若，则函数f(x)在(-¥,a]上的最小值为，且．

    当x≥a时，函数，

    若，则函数f(x)在[a，+¥ )上的最小值为，且．

    若时，则函数在[a,+¥ )上单调递增，从而函数f(x)在[a，+¥ )上的最小值为．

    综上所述，

    当时，函数f(x)的最小值为；

    当时，函数f(x)的最小值为；

    当时，函数f(x)的最小值为．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    设a为实数，函数f(x)=a
    		1-x2
    +
    		1+x
    +
    		1-x
    的最大值为g（a）．
    （1）求函数f（x）的定义域；
    （2）设t=
    		1+x
    +
    		1-x
    ，把函数f（x）表示为t的函数h（t），并写出定义域；
    （3）求g（a），并求当a＞-
    1
    2
    时满足g(a)=g(
    1
    a
    )    的实数a的取值集合．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设a为实数，函数f(x)=a
    		1-x2
    +
    		1+x
    +
    		1-x
    的最大值为g（a）．
    （1）求函数f（x）的定义域；
    （2）设t=
    		1+x
    +
    		1-x
    ，把函数f（x）表示为t的函数h（t），并写出定义域；
    （3）求g（a）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设a为实数，函数f(x)＝ex－2x＋2a，x∈R.

    (1)求f(x)的单调区间与极值；

    (2)求证：当a>ln2－1且x>0时，ex>x2－2ax＋1.

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年湖北省武汉市高三11月调考文科数学试卷（解析版） 题型：解答题

    设a为实数，函数f(x)＝ex－2x＋2a，x∈R．

    （Ⅰ）求f(x)的单调区间与极值；

    （Ⅱ）求证：当a＞ln2－1且x＞0时，ex＞x2－2ax＋1．

     

    查看答案和解析>>

    科目：高中数学 来源：2011年新疆乌鲁木齐市高二上学期期末考试理科数学卷 题型：解答题

    设a为实数，函数f(x)＝2x2＋(x－a)·|x－a|.

    (1)若f(0)≥1，求a的取值范围；

    (2)求f(x)的最小值；

    (3)设函数h (x)＝f(x)，x∈(a，＋∞)，直接写出(不需给出步骤)不等式h(x)≥1的解集．

     

    查看答案和解析>>

    同步练习册答案