
 )的值;
)的值; )的值与3的大小,并说明理由.
)的值与3的大小,并说明理由.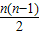 d=n2,又f(-1)=-a1+a2-a3+…-an-1+an=n,即
d=n2,又f(-1)=-a1+a2-a3+…-an-1+an=n,即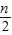 ×d=n,d=2,联立可得答案;
×d=n,d=2,联立可得答案; )=(
)=( )+3(
)+3( )2+5(
)2+5( )3+…+(2n-1)(
)3+…+(2n-1)( )n,将f(
)n,将f( )看成一个数列的前n项和,由错位相减法求解即可;
)看成一个数列的前n项和,由错位相减法求解即可; )=
)= -(2n+3)(
-(2n+3)( )n,易得f(
)n,易得f( )<
)< ,进而可得答案.
,进而可得答案.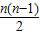 d=n2,即2a1+(n-1)d=2n.
d=n2,即2a1+(n-1)d=2n.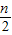 ×d=n,d=2.
×d=n,d=2. )=(
)=( )+3(
)+3( )2+5(
)2+5( )3+…+(2n-1)(
)3+…+(2n-1)( )n,①
)n,① ,可得
,可得 f(
f( )=(
)=( )2+3(
)2+3( )3+5(
)3+5( )4+…+(2n-1)(
)4+…+(2n-1)( )n+1,②
)n+1,② f(
f(  )=
)= +2(
+2(  )2+2(
)2+2(  )3+…+2(
)3+…+2(  )n-(2n-1)(
)n-(2n-1)(  )n+1,
)n+1, f(
f(  )=
)= +
+ +(
+(  )2+…+(
)2+…+(  )n-1-(2n-1)(
)n-1-(2n-1)(  )n+1.
)n+1. )=1+1+
)=1+1+ +
+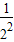 +…+
+…+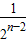 -(2n-1)
-(2n-1) =1+
=1+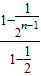 -(2n-1)
-(2n-1)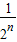 =1+2-
=1+2-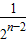 -(2n-1)
-(2n-1)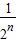 =3-(2n+3)(
=3-(2n+3)( )n;
)n; )=3-(2n+3)(
)=3-(2n+3)( )n;
)n; )=3-(2n+3)(
)=3-(2n+3)( )n,
)n, )n>0,
)n>0, )n<3,
)n<3, )<3.
)<3.

科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2011年高三数学复习(第2章 函数):2.15 函数的综合运用(解析版) 题型:解答题
 )与3的大小.
)与3的大小.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com