Question

【题目】已知椭圆，动圆：（圆心为椭圆上异于左右顶点的任意一点），过原点作两条射线与圆相切，分别交椭圆于，两点，且切线长最小值时,.

（Ⅰ）求椭圆的方程；

（Ⅱ）判断的面积是否为定值，若是，则求出该值；不是，请说明理由。

Answer 1

【答案】(Ⅰ) (Ⅱ)见解析

【解析】

（Ⅰ）由，所以当OP最小时切线长OT最小. 又切线长取最小值时,.，所以，，此时，再建立OP关于的函数，结合二次函数的最值情况可得.

（Ⅱ）先计算切线OM（或ON）斜率不存在时的面积，再计算OM、ON斜率都存在时设MN方程，直线方程与椭圆方程联立方程组，利用韦达定理求MN，求O到直线MN的距离，把的面积用k,m表示，再结合OM,ON与圆相切找出k,m的关系，化简可得.

（Ⅰ）

,又 在椭圆上， 得,

椭圆C的方程为：

（Ⅱ）解：（1）当切线OM或ON斜率不存在即圆P与y轴相切时，易得，代入椭圆方程得：说明圆P同时也与x轴相切，此时M、N分别为长、短轴一个端点，则的面积为

（2）当切线OM、ON斜率都存在时，设切线方程为：

由得：

整理得：

由韦达定理得：

设，由于点P不与点A、B重合时，直线的斜率存在，

不妨设直线的方程为：

将与椭圆方程联立可得：

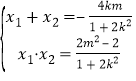
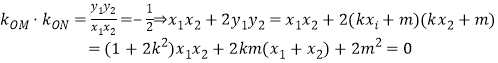
代入有：整理得：

又

而原点O到直线MN的距离为

所以的面积为定值.