|
|
|
已知函数f(x)= sinωx·cosωx-cos2ωx(ω>0)的最小正周期为 sinωx·cosωx-cos2ωx(ω>0)的最小正周期为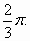
(Ⅰ)求ω的值;
(Ⅱ)设△ABC的三边a、b、c满足b2=ac,且边b所对的角为x,求此时f(x)的值域.
|
|
|
练习册系列答案
相关习题
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
已知二次函数f(x)=ax2-4bx+1,点(a,b)是区域 内的随机点,则函数y=f(x)在区间[1,+∞)上是增函数的概率为________. 内的随机点,则函数y=f(x)在区间[1,+∞)上是增函数的概率为________.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
已知双曲线的方程为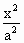 - -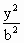 =1(a>0,b>0),双曲线的一个焦点到一条渐近线的距离为 =1(a>0,b>0),双曲线的一个焦点到一条渐近线的距离为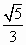 c(c为双曲线的半焦距长),则双曲线的离心率为 c(c为双曲线的半焦距长),则双曲线的离心率为
|
| [ ] |
A. |
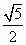
|
B. |
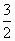
|
C. |
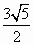
|
D. |
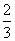
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
设随机变量ξ服从正态分布N(0,1),若P(ξ>1)=p,则P(-1<ξ<0)=
|
| [ ] |
A. |
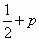
|
B. |
1-p
|
C. |
1-2p
|
D. |
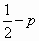
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
若函数f(x)=loga(x3-ax)>0且a≠1)在区间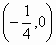 内单调递增,则实数a的取值范围是 内单调递增,则实数a的取值范围是
|
| [ ] |
A. |
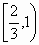
|
B. |
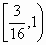
|
C. |
[ ,1)∪(1,3] ,1)∪(1,3]
|
D. |
(1,3]
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
已知函数f(x)=ln(ex+a)(e为常数)是R上的奇函数,函数g(x)=λf(x)+sinx是区间[-1,1]上的减函数.
(Ⅰ)求a的值;
(Ⅱ)若g(x)<t2+λt+1在x∈[-1,1]上恒成立,求t的取值范围;
(Ⅲ)讨论关于x的方程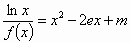 的根的个数. 的根的个数.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
若空间三条直线a、b、c满足a⊥b,b∥c,则直线a与c
|
| [ ] |
A. |
一定平行
|
B. |
一定相交
|
C. |
一定是异面直线
|
D. |
一定垂直
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
平面向量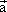 与 与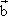 的夹角为60°, 的夹角为60°,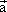 =(2,0),| =(2,0),|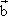 |=1,则| |=1,则|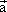 +2 +2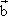 |= |=
|
| [ ] |
A. |
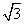
|
B. |
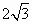
|
C. |
4
|
D. |
12
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
设i是虚数单位,若复数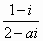 为实数,则实数a为 为实数,则实数a为
|
| [ ] |
A. |
2
|
B. |
-2
|
C. |
-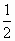
|
D. |
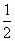
|
|
|
查看答案和解析>>
