
已知二次函数 在
在 处取得极值,且在
处取得极值,且在 点处的切线与直线
点处的切线与直线 平行.
平行.
(1)求 的解析式;
的解析式;
(2)求函数 的单调递增区间及极值。
的单调递增区间及极值。
(3)求函数 在
在 的最值。
的最值。
(1) (2)函数g(x)的单调递增区间为(﹣∞,
(2)函数g(x)的单调递增区间为(﹣∞, ),(1,+∞).在x2=1有极小值为0.在
),(1,+∞).在x2=1有极小值为0.在 有极大值
有极大值 .(3)函数g(x)的最大值为2,最小值为0.
.(3)函数g(x)的最大值为2,最小值为0.
【解析】
试题分析:(1)由f(x)=ax2+bx﹣3,知f′(x)=2ax+b.由二次函数f(x)=ax2+bx﹣3在x=1处取得极值,且在(0,﹣3)点处的切线与直线2x+y=0平行,知 ,由此能求出f(x).
,由此能求出f(x).
(2)由f(x)=x2﹣2x﹣3,知g(x)=xf(x)+4x=x3﹣2x2+x,所以g′(x)=3x2﹣4x+1=(3x﹣1)(x﹣1).令g′(x)=0,得 ,x2=1.列表讨论能求出函数g(x)=xf(x)+4x的单调递增区间及极值.
,x2=1.列表讨论能求出函数g(x)=xf(x)+4x的单调递增区间及极值.
(3)由g(0)=0,g(2)=2,结合(2)的结论,能求出函数g(x)的最大值和最小值.
试题解析:(1)由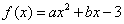 ,可得
,可得 . 由题设可得
. 由题设可得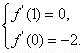 即
即
解得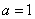 ,
,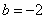 .所以
.所以 .
.
(2)由题意得 ,所以
,所以 .令
.令 ,得
,得 ,
, .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
| 4/27 |
| 0 |
|
所以函数g(x)的单调递增区间为(﹣∞, ),(1,+∞).在x2=1有极小值为0.
),(1,+∞).在x2=1有极小值为0.
在 有极大值
有极大值 .
.
(3)∵g(0)=0,g(2)=2,
∴由(2)知:函数g(x)的最大值为2,最小值为0.
考点:利用导数求闭区间上函数的最值;利用导数研究函数的单调性;利用导数研究函数的极值.


科目:高中数学 来源:2015届吉林省长春市高二下学期期末考试文科数学试卷(解析版) 题型:解答题
已知极坐标系的原点在直角坐标系的原点处,极轴为 轴正半轴,直线
轴正半轴,直线 的参数方程为
的参数方程为 (
( 为参数),曲线
为参数),曲线 的极坐标方程为
的极坐标方程为 .
.
(1)写出 的直角坐标方程,并说明
的直角坐标方程,并说明 是什么曲线?
是什么曲线?
(2)设直线 与曲线
与曲线 相交于
相交于 、
、 两点,求
两点,求 .
.
查看答案和解析>>
科目:高中数学 来源:2015届吉林省长春市高二下学期期中考试理科数学试卷(解析版) 题型:选择题
以下四个命题中:
①为了了解800名学生对学校某项教改试验的意见,打算从中抽取一个容量为 的
的
样本,考虑用系统抽样,则分段的间隔 为40;
为40;
②线性回归直线方程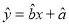 恒过样本中心
恒过样本中心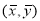 ,且至少过一个样本点;
,且至少过一个样本点;
③在某项测量中,测量结果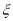 ~
~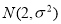 ,若
,若 在
在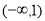 内取值的概率为
内取值的概率为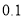 ,则
,则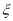 在
在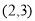 内取值的概率为
内取值的概率为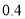 .其中真命题的个数为( )
.其中真命题的个数为( )
A.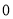 B.
B.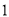 C.
C.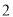 D.
D.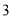
查看答案和解析>>
科目:高中数学 来源:2014-2015学年辽宁省高二第一次月考数学试卷(解析版) 题型:解答题
在 中,角
中,角 所对的边分别为
所对的边分别为 ,且
,且 .
.
(1)求角 的值;(2)若
的值;(2)若 为锐角三角形,且
为锐角三角形,且 ,求
,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年辽宁省高二第一次月考数学试卷(解析版) 题型:选择题
已知函数 的值域为[0,+∞),若关于x的不等式f(x)<c的解集为(m,m+6),则实数c的值为( )
的值域为[0,+∞),若关于x的不等式f(x)<c的解集为(m,m+6),则实数c的值为( )
A. 7 B. 8 C. 9 D. 10
查看答案和解析>>
科目:高中数学 来源:2014-2015学年辽宁省高二上学期10月模块考试数学试卷(解析版) 题型:填空题
关于数列有下列命题:
①数列{ }的前n项和为
}的前n项和为 ,且
,且 ,则{
,则{ }为等差或等比数列;
}为等差或等比数列;
②数列{ }为等差数列,且公差不为零,则数列{
}为等差数列,且公差不为零,则数列{ }中不会有
}中不会有 ,
,
③一个等差数列{ }中,若存在
}中,若存在 ,则对于任意自然数
,则对于任意自然数 ,都有
,都有 ;
;
④一个等比数列{ }中,若存在自然数
}中,若存在自然数 ,使
,使 ,则对于任意
,则对于任意 ,都有
,都有
 ,
,
其中正确命题的序号是___ __。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com