
【题目】△ABC的内角A,B,C所对的边分别为a,b,c, ![]() =(
=( ![]() ,1),
,1), ![]() =(sinA,cosA),
=(sinA,cosA), ![]() 与
与 ![]() 的夹角为60°. (Ⅰ)求角A的大小;
的夹角为60°. (Ⅰ)求角A的大小;
(Ⅱ)若sin(B﹣C)=2cosBsinC,求 ![]() 的值.
的值.
【答案】解:(Ⅰ)∵ ![]() =(
=( ![]() ,1),
,1), ![]() =(sinA,cosA),
=(sinA,cosA), ![]() 与
与 ![]() 的夹角为60°, ∴
的夹角为60°, ∴ ![]()
![]() =
= ![]() sinA+cosA=|
sinA+cosA=| ![]() ||
|| ![]() |cos60°,
|cos60°,
即2sin(A+ ![]() )=2×1×
)=2×1× ![]() =1,
=1,
即sin(A+ ![]() )=
)= ![]() ,
,
则A+ ![]() =
= ![]() 或
或 ![]() ,
,
则A=0(舍)或A= ![]() ;
;
(Ⅱ)若sin(B﹣C)=2cosBsinC,
则sinBcosC﹣cosBsinC=2cosBsinC,
即sinBcosC=3cosBsinC,
即tanB=3tanC,
即tan( ![]() ﹣C)=3tanC,
﹣C)=3tanC,
即 ![]() =3tanC,
=3tanC,![]() ﹣tanC=3tanC+3
﹣tanC=3tanC+3 ![]() tan2C,
tan2C,
即3 ![]() tan2C+4tanC﹣
tan2C+4tanC﹣ ![]() =0,
=0,
则tanC= 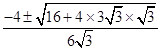 =
= =
![]() ,
,
∵B+C= ![]() ,∴0<C<
,∴0<C< ![]()
则tanC>0,∴tanC= ![]() ,
,
由sinBcosC=3cosBsinC,
得 ![]() =
= ![]() =
= 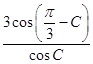 =
= 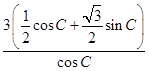 =
= ![]() +
+ ![]() ,
,
即 ![]() =
= ![]() +
+ ![]() =
= ![]() +
+ ![]() ×
× ![]() =
= ![]()
【解析】(Ⅰ)根据向量夹角公式以及向量数量积的坐标公式和定义建立方程关系进行求解解求角A的大小;(Ⅱ)若sin(B﹣C)=2cosBsinC,利用正弦定理以及两角和差的余弦公式进行化简整理即可求 ![]() 的值.
的值.
【考点精析】认真审题,首先需要了解余弦定理的定义(余弦定理:![]() ;
;![]() ;
;![]() ).
).


科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,
中, ![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() .
.
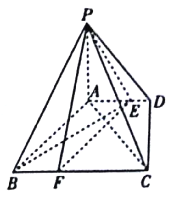
(Ⅰ)已知点![]() 在
在![]() 上,且
上,且![]() ,求证:平面
,求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)当二面角![]() 的余弦值为多少时,直线
的余弦值为多少时,直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对应的边分别为a,b,c,且(2a﹣c)cosB=bcosC. (Ⅰ)求角B的大小;
(Ⅱ)若 ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
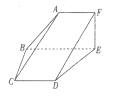
【题目】如图,平面![]() 平面
平面![]() 四边形
四边形![]() 为直角梯形,
为直角梯形, ![]() 四边形
四边形![]() 为等腰梯形,
为等腰梯形, ![]() 且
且![]()
(Ⅰ)若梯形![]() 内有一点
内有一点![]() ,使得
,使得![]() 平面
平面![]() ,求点
,求点![]() 的轨迹;
的轨迹;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
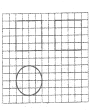
【题目】《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑,如图,网格纸上正方形小格的边长为![]() ,图中粗线画出的是某几何体毛坯的三视图,第一次切削,将该毛坯得到一个表面积最大的长方体,第二次切削沿长方体的对角面刨开,得到两个三棱柱,第三次切削将两个三棱柱分别沿棱和表面的对角线刨开得到两个鳖臑和两个阳马,则阳马与鳖臑的体积之比为( )
,图中粗线画出的是某几何体毛坯的三视图,第一次切削,将该毛坯得到一个表面积最大的长方体,第二次切削沿长方体的对角面刨开,得到两个三棱柱,第三次切削将两个三棱柱分别沿棱和表面的对角线刨开得到两个鳖臑和两个阳马,则阳马与鳖臑的体积之比为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线![]() 与圆
与圆![]() 交于M、N两点,且M、N关于直线
交于M、N两点,且M、N关于直线![]() 对称.
对称.
(1)求m,k的值;
(2)若直线![]() 与圆C交P,Q两点,是否存在实数a使得OP⊥OQ,如果存在,求出a的值;如果不存在,请说明理由.
与圆C交P,Q两点,是否存在实数a使得OP⊥OQ,如果存在,求出a的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,甲船从A处以每小时30海里的速度沿正北方向航行,乙船在B处沿固定方向匀速航行,B在A北偏西105°方向用与B相距10 ![]() 海里处.当甲船航行20分钟到达C处时,乙船航行到甲船的北偏西120°方向的D处,此时两船相距10海里.
海里处.当甲船航行20分钟到达C处时,乙船航行到甲船的北偏西120°方向的D处,此时两船相距10海里. 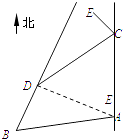
(1)求乙船每小时航行多少海里?
(2)在C的北偏西30°方向且与C相距 ![]() 海里处有一个暗礁E,周围
海里处有一个暗礁E,周围 ![]() 海里范围内为航行危险区域.问:甲、乙两船按原航向和速度航行有无危险?若有危险,则从有危险开始,经过多少小时后能脱离危险?若无危险,请说明理由.
海里范围内为航行危险区域.问:甲、乙两船按原航向和速度航行有无危险?若有危险,则从有危险开始,经过多少小时后能脱离危险?若无危险,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下四个命题:
①若 ![]() <
< ![]() <0,则
<0,则 ![]() +
+ ![]() >2;
>2;
②若a>b,则am2>bm2;
③在△ABC中,若sinA=sinB,则A=B;
④任意x∈R,都有ax2﹣ax+1≥0,则0<a≤4.
其中是真命题的有( )
A.①②
B.②③
C.①③
D.③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com