【题目】已知函数
.
（1）若
,讨论
的单调性;
（2）若
在
处取得极小值，求实数
的取值范围 .
【答案】（1） 
时，
在
上为增函数；
时，在
上单调递增，在
上单调递减；（2）
.
【解析】
试题分析：（1）先求函数
的导数
，再求函数
的导数
，分
、
、
分别讨论
符号，即可得到函数
的单调性；
（2）由（1）可知，时，
单调递增，恒满足
，且函数
在
处取得极小值，符合题意，当时， 在单调递增，且，故
即
时，函数在处取得极小值，符合题意，故可得
取值范围.
试题解析：（1） 
.
①时，当
时，
，所以在上为增函数；
②时，当时，，所以在上为增函数；
③时，令 
，得
，所以当
时，
；当
时，
，所以在上单调递增，在上单调递减；
综上所述，时，在上为增函数；时，在上单调递增，在上单调递减.
（2）
.当时，单调递增，恒满足，且函数在处取得极小值；
当时， 在单调递增，且，故即时，函数在处取得极小值.
综上所述，取值范围为.
教学练新同步练习系列答案
课前课后同步练习系列答案
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案科目：高中数学 来源： 题型：
【题目】已知各项均不相等的等差数列{an}的前四项和S4=14，且a1，a3，a7成等比数列．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设Tn为数列{
}的前n项和，若Tn≤λan+1对n∈N*恒成立，求实数λ的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数y=a+bx与
，若对于任意一点
，过点
作与X轴垂直的直线，交函数y=a+bx的图象于点
，交函数的图象于点
，定义：
，若
则用函数y=a+bx来拟合Y与X之间的关系更合适，否则用函数来拟合Y与X之间的关系
（1）给定一组变量P1(1,4),P2(2,5),p3(3,6),p4(4,5.5),p5(5,5.6),p6(6,5.8),对于函数
与函数
，试利用定义求Q1,Q2的值，并判断哪一个更适合作为点PI(xi,yi)(i=1,2,3…6)中的Y与X之间的拟合函数;
（2）若一组变量的散点图符合图象，试利用下表中的有关数据与公式求y对x的回归方程, 并预测当
时，
的值为多少.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中的
（附：对于一组数据
，其回归直线方程
的斜率和截距的最小二乘估计分别为
）
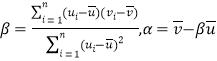查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图①，有一个等腰直角三角板
垂直于平面
，有一条长为7的细线，其两端分别位于
处，现用铅笔拉紧细线，在平面
上移动.
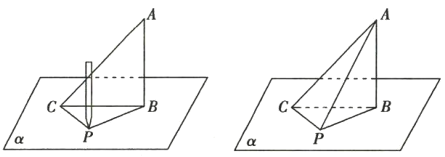
图① 图②
（1）图②中的
的长为多少时，
平面
？并给出证明.
（2）在（1）的情形下，求三棱锥
的高.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知一个几何体是由一个直角三角形绕其斜边旋转一周所形成的．若该三角形的周长为12米，三边长由小到大依次为a，b，c，且b恰好为a，c的算术平均数．
（1）求a，b，c；
（2）若在该几何体的表面涂上一层油漆，且每平方米油漆的造价为5元，求所涂的油漆的价格．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
