
分析 (1)化简方程,去掉绝对值即可;
(2)先去掉绝对值,把方程可化为x-|2x+1|=3①和x-|2x+1|=-3②,分别求出方程的解;
(3)讨论x的取值范围,去掉方程中的绝对值,求出原方程的解;
(4)把原方程化为|x-5|+|x-4|=1,讨论x的取值范围,去掉绝对值,求出方程的解.
解答 解:(1)∵3×|2x-1|-1=5,
∴3×|2x-1|=6,
∴|2x-1|=2,
∴2x-1=2或2x-1=-2,
解得x=$\frac{3}{2}$或x=-$\frac{1}{2}$;
(2)∵|x-|2x+1||=3,∴该方程可化为
x-|2x+1|=3①或x-|2x+1|=-3②,
由①得,x-3=|2x+1|,
两边平方得(x-3)2=(2x+1)2,
化简得3x2+10x-8=0,
解得x=-4或x=$\frac{2}{3}$,
经检验,x=-4和x=$\frac{2}{3}$都不是原方程的解;
由②得,x+3=|2x+1|,
两边平方得,(x+3)2=(2x+1)2,
解得x=2或x=-$\frac{4}{3}$,
经检验x=2和x=-$\frac{4}{3}$都是原方程的解;
综上,原方程的解为x=2或x=-$\frac{4}{3}$;
(3)∵|x-2|+|x+5|=6,
∴当x≥2时,方程化为(x-2)+(x+5)=6,解得x=$\frac{3}{2}$,不合题意,应舍去;
当-5<x<2时,方程化为(2-x)+(x+5)=6,即7=6,不合题意,应舍去;
当x≤-5时,方程化为(2-x)+(-x-5)=6,解得x=-$\frac{9}{4}$,不合题意,应舍去;
综上,该方程无解;
(4)∵|x-5|+$\sqrt{(4-x)^{2}}$=1,∴|x-5|+|x-4|=1
∴当x≥5时,方程化为(x-5)+(x-4)=1,解得x=5,满足题意;
当4<x<5时,方程化为(5-x)+(x-4)=1,即1=1,∴4<x<5,满足合题意;
当x≤4时,方程化为(5-x)+(4-x)=1,解得x=4,满足题意;
综上,该方程的解是[4,5].
点评 本题考查了含有绝对值的方程的解法与应用问题,解题的关键是去掉绝对值,是综合性题目.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案科目:高中数学 来源: 题型:解答题
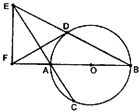 如图,AB是⊙O的直径,弦BD,CA的延长线相交于点E,EF垂直BA的延长线于点F.
如图,AB是⊙O的直径,弦BD,CA的延长线相交于点E,EF垂直BA的延长线于点F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overline{z}$=-1-i | B. | |$\overline{z}$|=$\sqrt{2}$ | C. | |$\overline{z}$|=2 | D. | $\overline{z}$=-1+i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
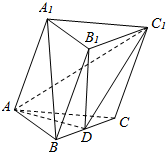 如图,三棱柱ABC-A1B1C1所有的棱长为2,B1在底面上的射影D在棱BC上,且A1B∥平面ADC1.
如图,三棱柱ABC-A1B1C1所有的棱长为2,B1在底面上的射影D在棱BC上,且A1B∥平面ADC1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com