Question

12．如图，PA⊥矩形ABCD所在的平面，M，N分别是PC，AB的中点，且PA=AB=2AD=4．
（1）求证：MN⊥CD；
（2）求四面体A-BMD的体积．

Answer 1

分析 （1）建立空间直角坐标系，求出$\overrightarrow{MN}$与$\overrightarrow{DC}$，$\overrightarrow{MN}•\overrightarrow{DC}=0$，从而MN⊥DC；
（2）利用等体积法来求，V_A-BMD=V_M-ABD；

解答 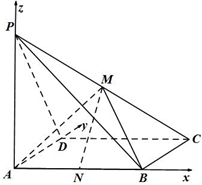解：（1）如图建立空间直角坐标系A-xyz，
则A（0，0，0），B（2，0，0），C（2，1，0），D（0，1，0），P（0，0，2），M（1，$\frac{1}{2}$，1），N（1，0，0）
∴$\overrightarrow{MN}$=（0，-$\frac{1}{2}$，-1），$\overrightarrow{DC}$=（2，0，0）
因为$\overrightarrow{MN}$•$\overrightarrow{DC}$=0，所以MN⊥CD．
（2）因为M，N分别是PC，AB的中点，且PA=AB=2AD=4；
        V_A-BMD=V_M-ABD
=$\frac{1}{3}$S_ABD•$\frac{1}{2}$PA
=$\frac{1}{3}$×$\frac{1}{2}$×AD×AB×$\frac{1}{2}$×PA=$\frac{8}{3}$．

点评 本题主要考查了空间直角坐标系、向量与多面体体积相关知识点，属简单题．