
| A. | 离心率相等 | B. | 焦距相等 | C. | 虚轴长相等 | D. | 顶点相同 |
分析 由双曲线的几何性质,即求得长轴,虚轴和焦距的值,利用同角三角函数的基本关系,即可求得答案.
解答 解:由曲线$\frac{x^2}{9}-\frac{y^2}{{4{{sin}^2}θ}}=1$,焦点在x轴上,长轴长为2a=6,虚轴长2b=4sinθ,
焦距为:2$\sqrt{9+4si{n}^{2}θ}$
与曲线$\frac{x^2}{{9-4{{cos}^2}θ}}-\frac{y^2}{4}=1$,焦点在x轴上,长轴长为2a=2$\sqrt{9-4co{s}^{2}θ}$,虚轴长2b=4,
焦距为:2$\sqrt{9-4co{s}^{2}θ+4}$$\sqrt{9+4(1-co{s}^{2}θ)}$=2$\sqrt{9+4si{n}^{2}θ}$,
故两者焦距相等,
故答案选:B.
点评 本题考查双曲线简单几何性质,同角三角函数的基本关系,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x2+2x+2≤0 | B. | 任意一个四边形的四个顶点共圆 | ||
| C. | ?x∈R,sin2x+cos2x=1 | D. | 所有能被3整除的整数都是奇数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=x,$g(x)=\sqrt{x{\;}^2}$ | B. | f(x)=x,$g(x)=\root{3}{x^3}$ | ||
| C. | f(x)=sinx,g(x)=sin(π+x) | D. | f(x)=x,g(x)=elnx |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
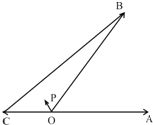 如图:已知$\overrightarrow{OC}=-\frac{1}{2}\overrightarrow{OA}$,若$\overrightarrow{OP}$的终点P在△OBC的边界及内部,且$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$则x、y满足的条件为( )
如图:已知$\overrightarrow{OC}=-\frac{1}{2}\overrightarrow{OA}$,若$\overrightarrow{OP}$的终点P在△OBC的边界及内部,且$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$则x、y满足的条件为( )| A. | $\left\{{\begin{array}{l}{-\frac{1}{2}≤x≤0}\\{0≤y≤1}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{x≤0}\\{y≥0}\\{y-2x-1≤0}\end{array}}\right.$ | ||
| C. | $\left\{{\begin{array}{l}{x≤0}\\{y≥0}\\{2y-x-1≤0}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{-\frac{1}{2}≤x≤0}\\{0≤y≤1}\\{y-2x-1≤0}\end{array}}\right.$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com