
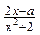 (x∈R).
(x∈R).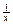 的两个实根为x1,x2,且-1≤a≤1,求|x1-x2|的最大值;
的两个实根为x1,x2,且-1≤a≤1,求|x1-x2|的最大值;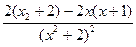 =
=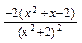 =
=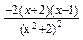 ≥0……………………4分
≥0……………………4分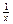 可化为x2-ax-2=0,Δ=a2+8 >0
可化为x2-ax-2=0,Δ=a2+8 >0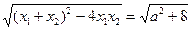
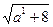 =3…………………………8分
=3…………………………8分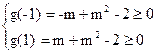 …………11分
…………11分

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源:不详 题型:解答题
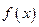 是定义在D上的函数,若对任何实数
是定义在D上的函数,若对任何实数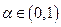 以及D中的任意两数
以及D中的任意两数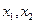 ,恒有
,恒有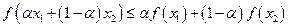 ,则称
,则称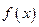 为定义在D上的C函数.
为定义在D上的C函数.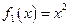 ,
,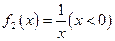 中哪些是各自定义域上的C函数,并说明理由;
中哪些是各自定义域上的C函数,并说明理由;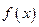 是R上的C函数,m是给定的正整数,设
是R上的C函数,m是给定的正整数,设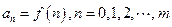 ,且
,且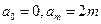 ,记
,记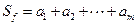 . 对于满足条件的任意函数
. 对于满足条件的任意函数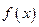 ,试求
,试求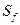 的最大值;
的最大值;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
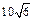 米(如图所示),旗杆底部与第一排在一个水平面上。若国歌长度约为50秒,问:升旗手应以多大的速度(米/秒)匀速升旗?
米(如图所示),旗杆底部与第一排在一个水平面上。若国歌长度约为50秒,问:升旗手应以多大的速度(米/秒)匀速升旗?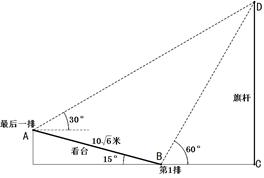
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,则a的取值范围是 ( )
,则a的取值范围是 ( )| A.R | B.(2,+∞) | C.[0,2] | D.(-∞,0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com